東大電子報第七期

我國、美國、韓國、中國大陸、歐洲及日本，均允許請求項中多項附屬項之存在(見以下表1)，至於是否允許多項附屬項間直接或間接依附，我國專利法施行細則第18 條第5 項規定：「多項附屬項間不得直接或間接依附」(以下，將「多項附屬項直接或間接依附於多項附屬項」之情形，簡稱為「多依多」)。

過去，除我國外，在國際上如美國、韓國與中國大陸等，亦禁止請求項中出現「多依多」之情形；而歐洲與日本，在過去則並未有相關之禁止規定。然而，從去年(2022 年)的4 月1 日起，日本亦開始立法規定，禁止請求項中出現「多依多」之情形，且其規定比我國更為嚴格，除「多項附屬項」外，甚至連「引用形式記載之獨立項」，亦會受到限制(見以下表1)。

＜表1：各國是否允許多項附屬項或「多依多」之比較＞

	TIPO	USPTO	KIPO	CNIPA	EPO	JPO
是否允許多 項附屬項？	Ｏ	Ｏ	Ｏ	Ｏ	Ｏ	Ｏ
是否允許多 依多？	X	Ｘ	Ｘ	Ｘ	Ｏ	Ｏ➜Ｘ (2022/4/1)

因此，在未來，主張日本優先權基礎案之台灣的發明專利申請案(新型專利申請案之情形，亦同，以下僅就發明專利申請案之情形予以說明)，亦將逐漸不再因為台日之間對於是否允許請求項中出現「多依多」的規定之不同，而有進一步配合台灣實務規定修正請求項之必要(因為日本目前的規定已比台灣更為嚴 格)；具體而言，從今年(2023 年)的 4 月 1 日起，理論上，主張日本優先權基礎案之台灣的發明專利申請案，其優先權日都是在 2022 年 4 月 1 日(從 2023 年 4月 1 日往前推一年)以後，因此，該優先權基礎案的請求項中並不會出現「多依多」之情形。

然而，若台灣的發明專利申請案主張的日本優先權基礎案，其優先權基礎日早於 2022 年 4 月 1 日，但於申請階段，在補正中文說明書時並未進行過主動修正以修正請求項中「多依多」之情形，則在進入實審階段後收到的審查意見通知函中，審查委員仍可能會依據專利法第 26 條第 4 項暨專利法施行細則第 18 條第5 項之規定，指摘請求項中有「多依多」之情事。

有鑑於此，在現時點(2023 年 4 月 1 日以後)，主張了日本優先權基礎案的台灣發明專利申請案，仍有可能需要在收到審查意見通知函時處理「多依多」之情形；而僅存的歐洲，於現時點亦仍允許請求項中存在「多依多」之情事，故主張了歐洲優先權基礎案的台灣發明專利申請案，亦有可能需要處理請求項中「多依多」之問題；因此，配合台灣之實務規定，處理主張了日本或歐洲的優先權基礎案的台灣發明專利申請案之請求項當中的「多依多」之問題，仍為擁有日本、歐洲客戶的台灣專利事務所的專利師、專利工程師，於日常的工作上時常會面臨的課題。

本所擁有許多日本客戶，因此，一直以來，在幫日本客戶申請主張日本優先權之台灣發明專利申請案時，時常有配合台灣實務規定修正請求項中「多依多」問題之需求。關於修正的時點，有的客戶傾向於在補正中文說明書的階段，就先進行請求項中「多依多」問題之主動修正；也有的客戶則習慣先不進行修正，待收到審查意見通知函之指摘時，再於申復時順便進行修正，以確保在核准前仍有一次確定請求項內容的機會(逕予核准之情形外)。

由於在補正中文說明書及申復階段均可能會處理到請求項中「多依多」的修正，因此，如何進行「多依多」之修正，亦成為本所新進專利工程師需要學習的課題之一。在補正中文說明書時修正「多依多」的情形，有的客戶會請本所工程師提供「多依多修正之提案」，亦有客戶會自行提出「多依多修正之提案」，再請我們確認內容是否正確；此時，有的客戶提供的「多依多修正之提案」中，會對於「引用形式記載之獨立項」亦進行了修正，而做出不必要的限縮。另外，在進行申復時修正「多依多」的情形，雖然不常發生，但亦有遇過審查意見通知函中指摘請求項中有「多依多」的情事，但經本所確認後，發現僅為審查委員之誤判，請求項中並未真的出現「多依多」之情事。

有鑑於專利申請人、專利審查委員均可能對「多依多」之修正方式做出誤判，而專利事務所的專利工程師在向客戶提出「多依多修正之提案」時，若請求項的依附關係相當複雜時，亦需花費相當長的時間進行思考及提案，因此，筆者在四年前的2019 年6 月，決定開發「多項附屬項間直接或間接依附之修正建議AI 程式」，以做為輔助本所工程師判斷請求項中是否有「多依多」之情形，並自動生成「多依多修正之提案」，供內部工程師參考之用。

在經過本所內部四年來反覆測試，證實了只要使用者正確地使用此AI 程式，其可以快速的判斷出請求項中有無多依多之情事，並且迅速而精確地生成「多依多修正之提案」，而大幅提升了本所工程師在進行相關的工作時之工作效率。

然而，為避免工程師尚失獨立思考、判斷之能力，雖然此程式輸出的結果幾乎不會有誤，我們仍要求工程師要盡量自行判斷後，再與程式輸出的結果進行核對，或是要對程式輸出的結果進行確認，而不允許在未經自行思考、確認的情況下，就直接使用AI 程式所輸出的「多依多修正建議」逕行向客戶提案。

我國專利法施行細則第18 條第5 項規定：「多項附屬項間不得直接或間接依附」。以下，將分別說明多項附屬項間「直接」依附，與「間接」依附之情形(見以下表2)。

＜表2：多項附屬項間「直接」或「間接」依附之比較＞

多項附屬項間「直接」依附	多項附屬項間「間接」依附
多項附屬項 ⇧ 多項附屬項	多項附屬項 ⇧ 單項附屬項 ⇧ 單項附屬項 ⇧ 多項附屬項

1、多項附屬項間「直接」依附之情形(以上表2 左欄)
多項附屬項間「直接」依附，指的是：

假設一附屬請求項同時依附於複數項以上的請求項，而為「多項附屬項」，此時，若此「多項附屬項」所依附之複數項以上的請求項當中，亦有另一項「多項附屬項」，則此二項「多項附屬項」之間，存在多項附屬項間「直接」依附之情事，而違反專利法施行細則第18 條第5 項之規定。

具體而言，若請求項共計4 項，其中，請求項1 為獨立項，請求項2~4 為附屬項，其依附關係如以下表3：

＜表3：多項附屬項間「直接」依附之具體例＞

【請求項1】
一種OO…。
【請求項2】
如請求項1 之OO，其中…。

【請求項3】
如請求項1 或2 之OO，其中…。
【請求項4】
如請求項1 至3 中任一項之OO，其中…。

此時，請求項 4 係依附於請求項 1 至 3 中任一項，為多項附屬項，而其所依附的請求項 3 係依附於請求項第 1 或 2 項，亦為多項附屬項。

因此，請求項 4 與請求項 3 之間，存在多項附屬項間「直接」依附之關係。

2、多項附屬項間「間接」依附之情形(以上表2 右欄)
多項附屬項間「間接」依附，指的是：
假設一附屬請求項同時依附於複數項以上的請求項，而為「多項附屬項」，此時，若此「多項附屬項」所依附之複數項以上的請求項當中，有一項「單項附屬項」，且
(1)、此「單項附屬項」又依附於另一項「多項附屬項」；或是
(2)、此「單項附屬項」雖然又依附於另一項「單項附屬項」，但此另一項「單項附屬項」又依附於另一項「多項附屬項」；或是
(3)、依此類推，此「單項附屬項」在經過一連串與「單項附屬項」之依附後，最終又依附於另一項「多項附屬項」。
則此二項「多項附屬項」之間，存在多項附屬項間「間接」依附之情事，而違反專利法施行細則第18 條第5 項之規定。
具體而言，若請求項共計5 項，其中，請求項1 為獨立項，請求項2~5 為附屬項，其依附關係如以下表4：

＜表4：多項附屬項間「間接」依附之具體例＞

【請求項1】
一種OO…。
【請求項2】
如請求項1 之OO，其中…。
【請求項3】
如請求項1 或2 之OO，其中…。
【請求項4】
如請求項3 之OO，其中…。
【請求項5】
如請求項2 或4 之OO，其中…。

此時，請求項5 係依附於請求項第2 或4 項，為多項附屬項，雖然其所依附的請求項4 係依附於請求項3，為單項附屬項，但請求項3 又依附於請求項第1 或2 項，亦為多項附屬項。

因此，請求項5 與請求項3 間，存在多項附屬項間「間接」依附之關係。

當存在多項附屬項間直接或間接依附之情形時，至少可進行「拆項修正」與「刪項修正」來解除多依多之情事。

以下，將先介紹第一種修正方式，也就是「拆項修正」。

「拆項修正」係將部分有多依多問題之附屬項，拆解成兩項以上之請求項，以解決多依多之問題，但不遺漏任何原揭露態樣。

若以表3 中「多項附屬項間直接依附」之情形作為「拆項修正」之具體案例，並追加表示其原有之揭露態樣(紅字部分)，可獲得以下表5：

＜表5：「拆項修正」之具體例＞

【請求項1】
一種OO…。
揭露態樣：1
【請求項2】
如請求項1 之OO，其中…。
揭露態樣：1+2
【請求項3】
如請求項1 或2 之OO，其中…。
揭露態樣：1+3、(1+2)+3
【請求項4】
如請求項1 至3 中任一項之OO，其中…。
揭露態樣：1+4、(1+2)+4、(1+3)+4、[(1+2)+3]+4

表5 中，假設請求項1~4 所揭露之技術特徵，分別為紅字之「1~4」。則：

(1)、請求項1 為獨立項，揭露了「1」之態樣；
(2)、請求項2 為依附於請求項1 之附屬項，故揭露了「1+2」之態樣；
(3)、請求項3 為依附於請求項1 或2 之附屬項，故揭露了「1+3」及「(1+2)+3」之態樣；
(4)、請求項4 為依附於請求項1 至3 中任一項之附屬項，故揭露了「1+4」、「(1+2)+4」、「(1+3)+4」及「[(1+2)+3]+4」之態樣；
而如前所述，請求項4 依附於請求項3 時，會發生「多依多」之情事，因此，若欲採用拆項修正，則需對於請求項3 或4 中之一者進行拆項，而至少有以下兩種拆項方式。

＜拆項方式I：對請求項4 進行拆項＞
將有多依多問題之請求項4，拆解為請求項4’及4”，如以下表6：

＜表6：拆項方式I＞

【請求項4】
如請求項1 至3 中任一項之OO，其中…。

揭露態樣：1+4、(1+2)+4、(1+3)+4、[(1+2)+3]+4
【請求項4’】
如請求項1 或2 之OO，其中…。
揭露態樣：1+4’、(1+2)+4′
【請求項4”】
如請求項3 之OO，其中…。
揭露態樣：(1+3)+4”、[(1+2)+3]+4”

從表6 中可發現，進行了拆項方式I 之拆項修正後，並未遺漏任何原揭露態樣(因為4、4’、4”為相同之技術特徵)。
然而，請求項中並不允許4’及4”之項次表現方式，因此，需將請求項4’之項次修正為4，並將請求項4”之項次修正為5，而得到以下修正完成之表7：

＜表7：拆項方式I 修正完畢＞

【請求項1】
一種OO…。
【請求項2】
如請求項1 之OO，其中…。
【請求項3】
如請求項1 或2 之OO，其中…。
【請求項4】
如請求項1 或2 之OO，其中…。
【請求項5】
如請求項3 之OO，其中…。

從表7 中可發現，唯二的多項附屬項請求項3 與4 之間，彼此並不存在依附關係，因此，經由拆項方式I 之修正後，表7 中修正後之請求項間已無多依多之情事發生。

＜拆項方式II：對請求項3 進行拆項＞
亦可將有多依多問題之請求項3，拆解為請求項3’及3”，並調整請求項4 之依附關係，如以下表8：

＜表8：拆項方式II＞

【請求項3】
如請求項1 或2 之OO，其中…。
揭露態樣：1+3、(1+2)+3
【請求項4】
如請求項1 至3 中任一項之OO，其中…。
揭露態樣：1+4、(1+2)+4、(1+3)+4、[(1+2)+3]+4
【請求項3’】
如請求項1 之OO，其中…。

揭露態樣：1+3′
【請求項3”】
如請求項2 之OO，其中…。
揭露態樣：(1+2)+3”
【請求項4】
如請求項1、2、3’、3”中任一項之OO，其中…。
揭露態樣：1+4、(1+2)+4、(1+3′)+4、[(1+2)+3”]+4

從表8 中可發現，進行了拆項方式II 之拆項修正後，亦未遺漏任何原揭露態樣(因為3、3’、3”為相同之技術特徵)。
同理，請求項中並不允許3’及3”之項次表現方式，因此，需將請求項3’之項次修正為3，將請求項3”之項次修正為4，將請求項4 之項次修正為5，而得到以下修正完成之表9：

＜表9：拆項方式II 修正完畢＞

【請求項1】
一種OO…。
【請求項2】
如請求項1 之OO，其中…。
【請求項3】
如請求項1 之OO，其中…。
【請求項4】
如請求項2 之OO，其中…。
【請求項5】
如請求項1~4 中任一項之OO，其中…。

從表9 中可發現，唯一的多項附屬項為請求項5，因此，經由拆項方式II 之修正後，表9 中修正後之請求項間已無多依多之情事發生。

＜進行拆項修正之優缺點＞
進行拆項修正之優點非常明顯，即為「不會遺漏任何原揭露態樣」，因此，能保留最完整的權利範圍。
然而，進行拆項修正亦存在以下缺點：
(1)、會改變原請求項的項次，而可能造成事後與客戶溝通時之不方便。
(2)、可能因請求項總項數的增加，而產生超項費用。
上述第(2)項缺點，在請求項中接連出現多項附屬項之情形，會使得拆項後的請求項總項數急遽增加。
以下，將以依附關係最大化(每一個附屬項都依附於前面所有請求項)之前提，對於「拆項後的請求項總項數急遽增加」之情形進行說明。

前面所舉的表3 的例子中，共僅有4 項請求項，其中請求項3、4 均為多項附屬項，筆者將表3 之情形稱為「連續兩項多依多」。

當請求項共有5 項且依附關係最大化時，則會出現以下表10 中「連續三項多依多」之情形：

＜表10：連續三項多依多＞

【請求項1】
一種OO…。
【請求項2】
如請求項1 之OO，其中…。
【請求項3】
如請求項1 或2 之OO，其中…。
【請求項4】
如請求項1 至3 中任一項之OO，其中…。
【請求項5】
如請求項1 至4 中任一項之OO，其中…。

此時，請求項3、4、5 均為多項附屬項，且出現以下三種多依多之情形：
(1)、請求項5 依附於請求項4 時
(2)、請求項5 依附於請求項3 時
(3)、請求項4 依附於請求項3 時
因此，若欲進行拆項修正，需從請求項3、4 或5 中，擇二進行修正，而有以下三種修正方式。
＜拆項方式IV：對請求項4、5 進行拆項＞
對請求項4、5 進行拆項後的結果，如以下表11 所示：

＜表11：連續三項多依多之拆項方式IV＞

【請求項1】
一種OO…。
【請求項2】
如請求項1 之OO，其中…。
【請求項3】
如請求項1 或2 之OO，其中…。
【請求項4’】
如請求項1 或2 之OO，其中…。
【請求項4”】
如請求項3 之OO，其中…。
【請求項5’】
如請求項1 或2 之OO，其中…。

【請求項5”】
如請求項3 之OO，其中…。
【請求項5”’】
如請求項4’之OO，其中…。
【請求項5””】
如請求項4”之OO，其中…。

此時，拆解過後的請求項共計9 項。

＜拆項方式V：對請求項3、4 進行拆項＞
對請求項3、4 進行拆項後的結果，如以下表12 所示：

＜表12：連續三項多依多之拆項方式V＞

【請求項1】
一種OO…。
【請求項2】
如請求項1 之OO，其中…。
【請求項3’】
如請求項1 之OO，其中…。
【請求項3”】
如請求項2 之OO，其中…。
【請求項4’】
如請求項1 之OO，其中…。
【請求項4”】
如請求項2 之OO，其中…。
【請求項4”’】
如請求項3’之OO，其中…。
【請求項4””】
如請求項3”之OO，其中…。
【請求項5】
如請求項1 至4””中任一項之OO，其中…。

此時，拆解過後的請求項亦為9 項。

＜拆項方式VI：對請求項3、5 進行拆項＞
對請求項3、5 進行拆項後的結果，如以下表13 所示：

＜表13：連續三項多依多之拆項方式VI＞

【請求項1】
一種OO…。
【請求項2】
如請求項1 之OO，其中…。
【請求項3’】
如請求項1 之OO，其中…。
【請求項3”】
如請求項2 之OO，其中…。
【請求項4】
如請求項1 至3”中任一項之OO，其中…。
【請求項5】
如請求項1 至3”中任一項之OO，其中…。
【請求項5’】
如請求項4 之OO，其中…。

此時，拆解過後的請求項竟然僅有7 項，較前面兩種拆法(均為9 項)來的少，見以下表14。

＜表14：連續三項多依多之拆項後總項數＞

拆項對象	總項數
請求項 4、5(不拆請求項 3)	9
請求項 3、5(不拆請求項 4)	7
請求項 3、4(不拆請求項 5)	9

在此，筆者基於個人興趣，想研究一下對於「依附關係最大化之連續多項多依多請求項」，應如何拆解，才能獲得最小總項數，以降低超項費。
首先，對於以下表15 中連續四項多依多之拆項後總項數進行分析。

＜表15：連續四項多依多＞

【請求項1】
一種OO…。
【請求項2】
如請求項1 之OO，其中…。
【請求項3】
如請求項1 或2 之OO，其中…。
【請求項4】
如請求項1 至3 中任一項之OO，其中…。
【請求項5】

如請求項1 至4 中任一項之OO，其中…。
【請求項6】
如請求項1 至5 中任一項之OO，其中…。

此時，若欲進行拆項修正，需從請求項3、4、5 或6 中，擇三進行修正，而有四種修正方式，對應的總項數如以下表16 所示(在此，省略詳細拆項細節，僅提供結論)。

＜表16：連續四項多依多之拆項後總項數＞

拆項對象	總項數
請求項 4、5、6(不拆請求項 3)	17
請求項 3、5、6(不拆請求項 4)	11
請求項 3、4、6(不拆請求項 5)	11
請求項 3、4、5(不拆請求項 6)	17

從表14 連續三項多依多及表16 連續四項多依多之情形來看，均為不對中間項進行拆項(偶數項時為中間兩項中任一項)，總項數最小。
為了證明我們觀察到的上述現象係正確，我們設定了以下專題：
＜研究主題＞
當請求項1 為獨立項，其後所有附屬項都依附於前面所有請求項時(亦即，依附關係最大化之情形)，
(1)、應如何拆項修正，方可使修正後之總項數最少？
(2)、拆項修正後之總項數如何增長？
＜主題(1)、應如何拆項修正，方可使修正後之總項數最少？＞
答案：不拆解最中間項(或偶數時，最中間兩項之任一項)，拆項後的總項數最少。
前面的案例中，我們知道請求項有4 項時，對第3 或4 項進行拆項後的總項數均為5 項；請求項有5 項時，不同方式拆項後的總項數分別為9、7、9 項；請求項有6 項時，不同方式拆項後的總項數分別為17、11、11、17 項。
因此，若假設原總項數為n，未被選擇進行拆項者(亦稱為「未修項」)為第m 項(m＞2，且m＜=n)，此時，我們可以將上述「表7 及表9」、表14、表16 之依不同方式拆項後的總項數，整理為以下表17。

＜表17：n=4~6 時，拆項修正後之總項數＞

修正方式	未修項 m	原總項數 n=4	原總項數 n=5	原總項數 n=6
修正第 4~n 項(修正第 3~n 項， 但不修正第 m 項。其中 m=3)	m=3	拆項修正後之總項數=5	拆項修正後之總項數=9	拆項修正後之總項數=17
修正第 3~n 項， 但不修正第 m 項。	m=4		拆項修正後之 總項數=7	拆項修正後之 總項數=11
其中 m=4..n-1	m=5			拆項修正後之 總項數=11
修正第 3~n-1 項(修正第 3~n 項，但不修正第 m 項。其中 m=n)	m=n	拆項修正後之總項數=5	拆項修正後之總項數=9	拆項修正後之總項數=17

表17 乍看之下雖然有些複雜，但其實其使用方式及傳達的訊息均不困難。
具體而言，第一欄係顯示修正方式，當原總項數n=6 時，共有四種修正方式，分別為：「修正第4~6 項」、「修正第3~6 項，但不修正第4 項」、「修正第3~6 項，但不修正第5 項」以及「修正第3~5 項」。
第二欄係換個方式說明修正方式，也就是係以「未修正(未拆項)哪一項？」進行說明，此m 需＜=n，當m＞n 時「拆項修正後之總項數」的欄位會是空白的，當m=n 時則會填寫於最下方的欄位。例如，當原總項數n=6 時，共有四種修正方式，分別為：「不修正第3 項、「不修正第4項」、「不修正第5 項」以及「不修正第6 項」。
第三欄係顯示原總項數n=4 時之情形。當修正第4 項(不修正第3 項時)，「拆項修正後之總項數」為5；當修正第3 項(不修正第4 項時)，「拆項修正後之總項數」亦為5。
第四欄係顯示原總項數n=5 時之情形。當修正第4、5 項(不修正第3 項時)，「拆項修正後之總項數」為9；當修正第3、5 項(不修正第4 項時)，「拆項修正後之總項數」為7；當修正第3、4 項(不修正第5 項時)，「拆項修正後之總項數」為9。
第五欄係顯示原總項數n=6 時之情形。當修正第4、5、6 項(不修正第3 項時)，「拆項修正後之總項數」為17；當修正第3、5、6 項(不修正第4 項時)，「拆項修正後之總項數」為11；當修正第3、4、6 項(不修正第5 項時)，「拆項修正後之總項數」為11；當修正第3、4、5 項(不修正第6 項時)，「拆項修正後之總項數」為17。
經過以上的說明，相信各位已經熟悉表17 之記載方式，在此，我們要一口氣將n=4~15 的情形一次揭露於以下的表18(省略與表17 中同樣的說明文字)。

＜表18：原總項數n=4~15 時，拆項修正後之總項數＞

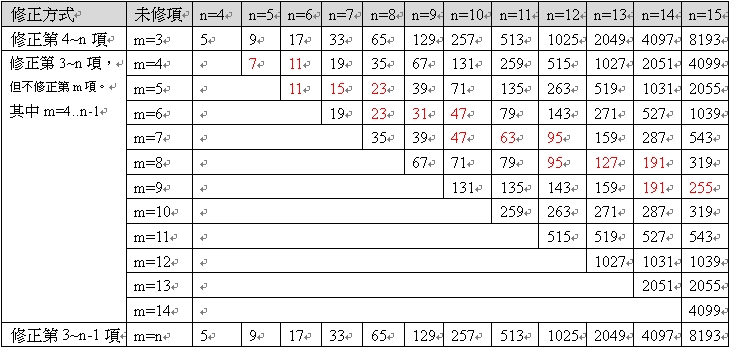
以上的表18 中，從左側數來第九欄顯示了原總項數n=10 時之情形。此時，不修正第3 項至不修正第10 項等八種不同的修正方式，所得到的拆項修正後之總項數分別為：257、131、71、47、47、71、131 及257，亦即，m=6 或7 時(不修正第6 項或第7 項)，修正後之總項為最少，為47 項。
又例如，表18 中，從左側數來第十四欄(從右側數來第一欄)顯示了原總項數n=15 時之情形。此時，不修正第3 項至不修正第15 項等十三種不同的修正方式，所得到的拆項修正後之總項數分別為：8193、4099、2055、1039、543、319、255、319、543、1039、2055、4099 及8193，亦即，m=9 時(不修正第9 項)，修正後之總項為最少，為255 項。
表18 中，如同以上所舉例之n=10 及n=15 之情形，拆項修正後之總項數最少者，均以紅字表示。例如，n=5 時為7，n=6 為11、11，n=7 為15，n=8 為23、23…。
因此，我們可得出＜第一個結論＞：不拆解最中間項(或偶數項時，最中間兩項中任一項)，修正後之總項數為最少。另外，若以第二列，亦即m=3 時來看，我們可以發現，隨著n 的增加，修正後總項數係呈指數成長，如以下表19：

＜表19：m=3 時，不同原總項數n 值所對應之拆項修正後總項數＞

n	4	5	6	7	8	9	10	11	12	13	14	15
拆項修正 後總項數	5	9	17	33	65	129	257	513	1025	2049	4097	8193

從表19 中我們可以發現，在m=3，亦即不對第三項進行拆項時，隨著原總項數n 值增加，拆項修正後的總項數係呈指數增加，我們可將之一般化為以下【式1】：
2^(n-2)+1……【式1】
透過上述【式1】，我們可驗證表19 中，例如n=15 時，拆項修正後總項數為2^(15-2)+1=8193，我們亦可進行一步推得表19 中不存在的n=16 時的拆項修正後總項數，應為2^(16-2)+1=16385。
若將表19 之「第二欄m=3~n」對於「不同的原總項數n」，均整理出「拆項修正後總項數」的一般式(例如，上述【式1】即為m=3 時之「拆項修正後總項數」的一般式)，可得到以下表20：

＜表20：m=3~n 時，不同原總項數n 值所對應之拆項修正後總項數一般式及限制＞

修正方式	未修項 m	修正後之總項數一般式 (其中 n 為原總項數)	一般式限制
修正第 4~n 項	m=3	2^(n-2)+1	n＞=4
修正第 3~n 項， 但不修正第 m 項。其中 m=4..n-1	m=4	2^(n-3)+3	n＞=5
	m=5	2^(n-4)+7	n＞=6
	m=6	2^(n-5)+15	n＞=7
	m=7	2^(n-6)+31	n＞=8
	m=8	2^(n-7)+63	n＞=9
	m=9	2^(n-8)+127	n＞=10
	m=10	2^(n-9)+255	n＞=11
	m=11	2^(n-10)+511	n＞=12
	m=12	2^(n-11)+1023	n＞=13
	m=13	2^(n-12)+2047	n＞=14
	m=14	2^(n-13)+4095	n＞=15
修正第 3~n-1 項	m=n	2^1+[2^(n-2)-1] 即 2^(n-2)+1	n＞=4

以上表20 中之第二列即為上述【式1】之情形，【式1】之限制為n＞=4，其理由可從表18、19 中得知。
表20 的第三列係對應到表18 的第三列中m=4 之情形，為了再次舉例說明，此次以表18 第三列中m=4 時為例進行觀察，可發現隨著n 的增加，修正後總項數亦呈指數成長，整理如以下表21：

＜表21：m=4 時，不同原總項數n 值所對應之拆項修正後總項數＞

n	5	6	7	8	9	10	11	12	13	14	15
拆項修正 後總項數	7	11	19	35	67	131	259	515	1027	2051	4099

從表21，我們可以理解表20 之第二列中將m=4 之一般式定為以下【式2】之理由：
2^(n-3)+3……【式2】
例如，n=11 時，代入【式2】，拆項修正後總項數2^(11-3)+3=259，符合表21 或表18 中之記載，我們亦可從表21 及表18 中理解【式2】之限制條件為n＞=5 之理由。
接著，我們亦可從表20 的第三欄「修正後之總項數一般式(其中n為原總項數)」隨著m 值的變化，再次將「修正後之總項數」公式整理為以下【式3】中，更為一般化之以n 與m 為變數的公式：修正後之總項數通式：2^[n-(m-1)]+[2^(m-2)-1]……【式3】(上式中，n 為原總項數，m 為未修項)

例如，當m=3 時，代入【式3】
2^[n-(3-1)]+[2^(3-2)-1]=2^(n-2)+1，即為【式1】

又例如，當m=4 時，代入【式3】
2^[n-(4-1)]+[2^(4-2)-1]=2^(n-3)+3，即為【式2】
綜上所述，從表20 中，我們可得出＜第二個結論＞：拆項修正後的總項數(不論m 值為何)，係隨連續多依多的次數增加，而呈指數成長。
亦即，係呈以下【式4】中之指數關係：拆項後總項數= 2−+b (其中，n 為原總項數，a、b 為常數 )……【式4】
以下圖1 中，我們將不同的m 值時，「原總項數n 值」所對應之「拆項修正後總項數」之指數關係，直接繪圖呈現。
從圖1 中可以發現：
當n=15 時，m=3 或15 時，「拆項修正後總項數」有最大值8193；
當n=15 時，m=9 時，「拆項修正後總項數」有最小值255。
此事實亦可對應於表18 中，從左側數來第十四欄(從右側數來第一欄)顯示之原總項數n=15 時之情形。

＜圖1：不同m 時，原總項數n 值所對應之拆項修正後總項數＞

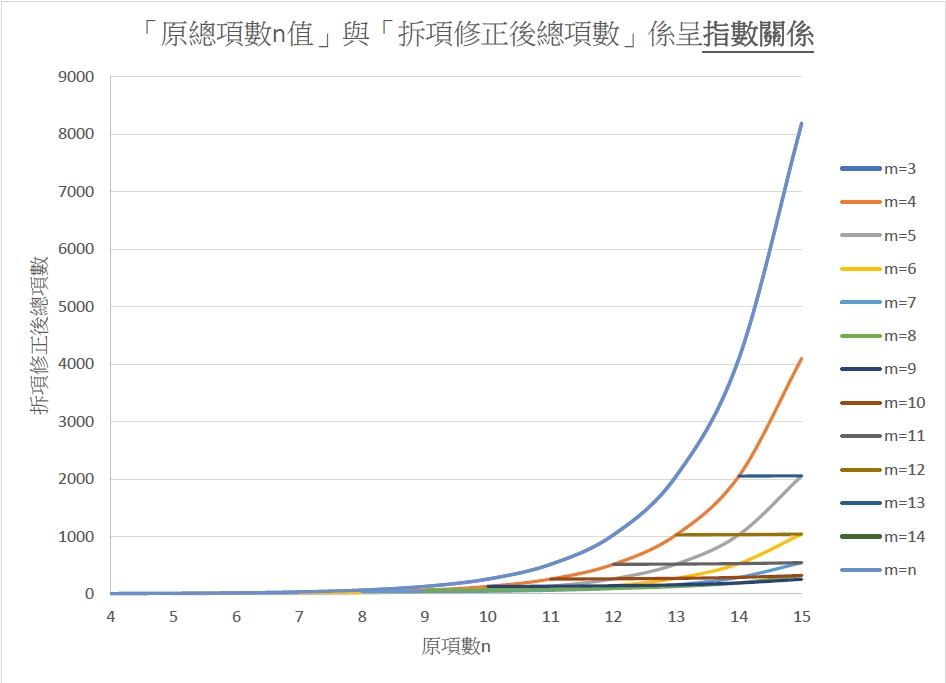
從圖1 中，我們再次驗證上述兩個結論：
＜第一個結論＞：不拆解最中間項(或偶數項時，最中間兩項中任一項)，修正後之總項數為最少。
例如，上述n=15 時，修正後總項數的最小值發生在m=9，亦即m=(3+15)/2。而最大值發生在m=3 或15 時。

＜第二個結論＞：如圖1，拆項修正後的總項數(不論m 值為何)，係隨連續多依多的次數增加，也就是原總項數n 值的增加，而呈指數成長。

＜進行拆項修正之可行性＞
基於以上＜第二個結論＞，我們再次考量拆項修正之可行性。
若依以上＜第一個結論＞，拆解修正後總項數之最大值m=3 時為例行說明，並參照表19，我們知道，當原總項數n 從4、5、6、7…增加時，修正後總項數係如下【數列1】變化：
5→9→17→33→2−2+1……【數列1】
其中，m=3，n=6 時，修正後總項數為17。
具體而言，這17 項請求項之依附關係係如以下表22 所示：

＜表22、n=6，m=3 時，修正後總項數共計17 項＞

【請求項1】
一種OO…。
【請求項2】
如請求項1 之OO，其中…。
【請求項3】
如請求項1 或2 之OO，其中…。
【請求項4’】
如請求項1 或2 之OO，其中…。
【請求項4”】
如請求項3 之OO，其中…。
【請求項5’】
如請求項1 或2 之OO，其中…。
【請求項5”】
如請求項3 之OO，其中…。
【請求項5”’】
如請求項4’之OO，其中…。
【請求項5””】
如請求項4″之OO，其中…。

【請求項6’】
如請求項1 或2 之OO，其中…。
【請求項6”】
如請求項3 之OO，其中…。
【請求項6”’】
如請求項4’之OO，其中…。
【請求項6””】
如請求項4″之OO，其中…。
【請求項6””’】
如請求項5’之OO，其中…。
【請求項6”””】
如請求項5”之OO，其中…。
【請求項6”””’】
如請求項5”’之OO，其中…。
【請求項6””””】
如請求項5””之OO，其中…。

這還僅為原總項數只有6 項之情形，修正後的總項數就多達17 項了。
若為原總項數為10 項的情形，修正前的請求項如下表23 所示：

＜表22、n=10 時，修正差原總項數為10 項＞

【請求項1】
一種OO…。
【請求項2】
如請求項1 之OO，其中…。
【請求項3】
如請求項1 或2 之OO，其中…。
【請求項4】
如請求項1 至3 中任一項之OO，其中…。
【請求項5】
如請求項1 至4 中任一項之OO，其中…。
【請求項6】
如請求項1 至5 中任一項之OO，其中…。
【請求項7】
如請求項1 至6 中任一項之OO，其中…。
【請求項8】
如請求項1 至7 中任一項之OO，其中…。
【請求項9】
如請求項1 至8 中任一項之OO，其中…。

【請求項10】
如請求項1 至9 中任一項之OO，其中…。

此時，依表18 左側數來第九欄所示，拆解後的總項數共計47~257 項。
若故意逆其道而行，以拆項後總項數最大化來看，係不對於第3 項進行拆項(即拆解「請求項4~10 項」)或不對於第10 項進行拆項(即拆解「請求項3~9 項」)，此時，拆項後總項數為257 項，至少(不含主動修正或申復時又新增)超項247 項，產生超項費247×800=NTD197,600。
若利用上述＜第二個結論＞，改為不拆解最中間項(m=6 或7)，亦即拆解「請求項3~5 及7~10 項」或「請求項3~6 及8~10 項」，則拆項後僅增為47 項，超項37 項，超項費為37×800=NTD29,600，相較於257 項之情形，可省下NTD168,000。

＜拆項修正之問題1-超項費極高＞
然而，無論如何極力降低修正後之總項數，連續多依多時，若欲不遺漏任何樣態而使用拆項修正，仍會產生極高之超項費用，例如上述表22 中請求項為10 項之情況，拆項後的總項數因拆解方式的不同而為47~257 項，產生的超項費為NTD29,600~197,600；若項數再增加5 項，以原總項數為15 項之情形為例，查詢表18，拆解後的總項數因拆解方式的不同為255~8193 項，產生的超項費為NTD203,200~6,546,400，亦即數十萬元至數百萬元，此時，基於預算合理性的考量，跟本不可能用拆項的方式進行修正。
＜拆項修正之問題2-若為其它依附關係時，拆解方式將更為複雜＞
除了費用面的考量外，若非上述較為規律之「依附態樣最大化」(每一個附屬項都依附於前面所有請求項)的依附關係，而為其它依附關係時，又該如何進行拆項修正，方能保有所有原依附態樣，又能使拆解後總項數最少呢？
由於此問題非常複雜，且拆解後的總項數，在多項附屬項連續依附時，依然會非常多，因此，讓我們直接進入下一主題：「刪項修正」。

考量到前述「拆項修正」的方式在多項附屬項連續依附時，可能造成修正後的總項數過多，進而產生高額之超項費用；且如前所述，依附關係複雜時，並不容易理解「如何拆解才能獲得最少之修正後總項數？」，權衡之下，使用「刪項修正」，也就是「刪除原依附關係中，部分的依附項次」之修正方式，雖無法保有所有原依附態樣，但可避免前述問題點之產生。
「刪項修正」之修正方式，除了用「刪除原依附關係中，部分的依附項次」來理解外，亦相當於在先前之「拆項修正」後，僅留下某請求項(例如前述請求項4)拆解後的其中一項請求項(例如前述請求項4′)，而刪除剩餘請求項(例如前述請求項4”)。

＜刪項修正之方式＞
正如同前述「拆項修正」時有不同的方式(不同m 值)，「刪項修正」之方式亦非固定。
例如，以前述「依附態樣最大化」之情形為例，若請求項共計4 項，其中第3 項及第4 項為多項附屬項，此時：
＜條件1＞欲對第3 項及第4 項中之何項進行刪項(依附項的刪減)？
＜條件2＞欲刪減的又是其中的哪些依附項？

上述＜條件1＞及＜條件2＞的選擇方式並無標準答案，在此，筆者先進行一假設，並以此假設為前提，來進行＜條件1＞及＜條件2＞的選擇。

在此，筆者假設：在一獨立項與其複數附屬項所構成之一請求項群組中，愈重要的技術特徵，其請求項項次係被安排在愈前面。例如，請求項1 為獨立項，請求項2~5 為請求項1 直接或間接之附屬項，則假設各請求項所揭露的技術特徵之重要性，係隨著請求項的項次之增大(1 -> 5)，而遞減。

在此前提下，在上述＜條件1＞的選擇上：
＜原則1＞我們會盡量保留項次較前的請求項，並選擇「項次較後面的請求項」，進行「刪項」修正。
同時，在＜條件2＞的選擇上：
＜原則2＞對於選定要刪項的請求項，我們亦會保留項次較前的依附對象，並刪除所依附的項次中「項次較後面者」。
藉由以上＜原則1＞及＜原則2＞，並配合前述假設，可滿足「通常愈重要的技術特徵，其項次安排上係在愈前面，故應該盡量予以保留」之期待，並可將刪項修正的修正方式標準化(依此規則，不論由任何人來進行，均會得到一樣之結果)，進而，可將此標準化後之程創建為AI 程式，以提高工作效率及精確性。
上述＜原則1＞更具體而言，若一獨立項與其複數附屬項所構成之一請求項群組中，存在兩項以上的多項附屬項，則不對第一項(項次最為前面)多項附屬項進行刪項，而係對其它多項附屬項進行刪項。
上述＜原則2＞更具體而言，若欲對一選定之多項附屬項進行刪項，則不對其所依附的請求項中第一項(項次最為前面)的依附對象進行刪項，並在不會產生多依多的前提下，盡可能的保留其原先所依附的對象，僅刪除必要刪除的依附對象。

上述兩段說明雖然已解釋完「刪項修正」的精髓，但不搭配案例說明恐仍難理解，讓我們於以下表23 中，再次使用與表5 相同之例子進行「刪項修正」的說明。

＜表23：「刪項修正」之具體例＞

【請求項1】
一種OO…。
揭露態樣：1
【請求項2】
如請求項1 之OO，其中…。
揭露態樣：1+2
【請求項3】
如請求項1 或2 之OO，其中…。
揭露態樣：1+3、(1+2)+3
【請求項4】
如請求項1 至3 中任一項之OO，其中…。
揭露態樣：1+4、(1+2)+4、(1+3)+4、[(1+2)+3]+4

表23 中，請求項3、4 均為多項附屬項，請求項4 依附於請求項3時，會產生「多依多」之情事，此時，需對於請求項3 或4 其中一項進行「刪項修正」，而基於上述＜原則1＞，我們選擇「項次較為後面的請求項4」進行修正。

請求項4 原先係依附於請求項1~3 中任一項，基於上述＜原則2＞，我們至少會保留請求項4 依附於請求項1~3 中項次最前面的依附對象，也就是「請求項4 依附於請求項1」的態樣。
然而，若將請求項4 由「依附於請求項1~3 中任一項」修正為「依附於請求項1」，又過度限縮了，因此，我們又基於＜原則2＞中，「在不會產生多依多的前提下，盡可能的保留其原先所依附的對象，僅刪除必要刪除的依附對象」之次原則，而亦保留了「請求項4 依附於請求項2」的態樣。
最終，對於表23 中之情形，進行了刪項修正後，我們得到了以下表24：

＜表24：對於表23 之請求項進行完「刪項修正」後之請求項＞

【請求項1】
一種OO…。
揭露態樣：1
【請求項2】
如請求項1 之OO，其中…。
揭露態樣：1+2
【請求項3】
如請求項1 或2 之OO，其中…。

揭露態樣：1+3、(1+2)+3
【請求項4】
如請求項1 或2 之OO，其中…。
揭露態樣：1+4、(1+2)+4、(1+3)+4、[(1+2)+3]+4

修正後之表24 中的請求項已不見多依多之情形，然而，亦放棄了原揭露態樣中的「(1+3)+4 及[(1+2)+3]+4」兩種揭露態樣。
再次說明，上述表24 並非唯一的刪項方式，如果刻意違反＜原則l＞與＜原則2＞，亦可獲得不同之修正方式，整理如以下表25：

＜表25：對於表23 之請求項進行之其它「刪項修正」方式＞

＜原則 l＞	＜原則 2＞	修正方式
Ｏ	Ｏ	【請求項 4】 如請求項 1 或 2 之 OO，其中…。(亦即，表 24 之結果)
Ｏ	Ｘ	【請求項 4】 如請求項 3 之 OO，其中…。
Ｘ	Ｏ	【請求項 3】 如請求項 1 之 OO，其中…。
Ｘ	Ｘ	【請求項 3】 如請求項 2 之 OO，其中…。

表25 的四種「刪項修正」方式，均可克服表23 中「多依多」之情事，但以下，我們還是僅以符合＜原則l＞與＜原則2＞之情形進行討論。
＜進行刪項修正之優缺點＞
進行「刪項修正」之優點，恰與「拆項修正」之缺點相反，為「不會改變請求項之原項次(故易於跟客戶溝通)，且不會增加請求項總項數(總項數不變，故不會增加超項費)。
而「刪項修正」之缺點，亦與「刪項修正」之優點相反，為「無法保留完整的原權利範圍」。

以下，將依序說明筆者研發之「多依多修正AI 程式」(符合＜原則1＞、＜原則2＞之「刪項修正」方式)的設計原理及使用方式。
＜設計原理＞
以下，將舉實際案例說明「多依多之修正建議AI 程式」的設計原理。以下案例的依附關係將不在像前述「依附態樣最大化」(每一個附屬項都依附於前面所有請求項)的依附關係那般規律、單純，而係更為複雜之一般情況。

事實上，此AI 程式可應付大多數一般之複雜依附關係，但暫不討論「跨項依附」這種不符合法規之情形，或是「如『依附於請求項2 之』請求項3 之OO」這種特殊情形(除上述兩種情形外，此AI 程式基本上可應付任何依附關係)。
以下表26 為一個依附關係略顯複雜之「獨立項與其直接或間接之附屬項所構成之請求項群」：

＜表26：多依多之修正建議AI 範例＞

請求項	1	2	3	4	5	6	7	8	9	10
依附關係	獨立項	1	1,2	3	1~4	2~5	3~6	2,6	6~8	1~9

表26 中，第一列顯示請求項之項次，第二列顯示其為獨立項，或是以數字表示其為附屬項及所依附之項次。
例如，表26 中，請求項1 為獨立項，請求項2 為依附於請求項1 之附屬項，請求項3 為依附於請求項1 或2 之附屬項，依此類推。
針對表26 中的情形，AI 程式會開一個陣列，去紀錄每一個請求項的「多項狀態」，及每一個請求項之依附關係，如以下表27：

＜表27：多依多修正AI 程式之陣列＞

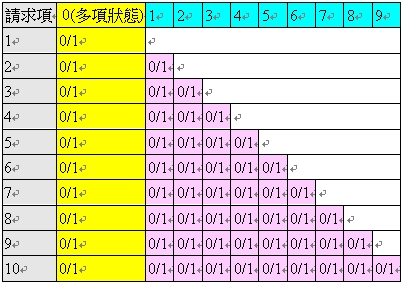
表27 中，第一欄表示請求項的項次；第二欄(黃色欄位)表示各請求項的「多項狀態」，有0 與1 兩種狀態，細節將於後述；第三欄表示各請求項是否依附於請求項1，有0 與1 兩種情形，0 表示未依附，1 表示有依附；同理，第四~十一欄分別表示各請求項是否依附於請求項2~9，亦以0 與1 來表示是否依附。亦即，第一列右側的1~9(藍色欄位)，係記
錄各請求項之「依附關係」。
上述第二欄「多項狀態」之0 與1 值，係由AI 程式判斷填入，而上述第三~十一欄「是否依附於前面的請求項」之0 與1 值，在起始時，係先由使用者輸入「修正前請求項之依附狀況」，後續再由AI 調整為「修正後請求項之依附狀況」。

上述「多項狀態」，係用以判斷該請求項在修正之後，是否為「多項附屬項」或是「直接或間接依附於多項附屬項之單項附屬項」，其在陣列中的位置(y 位置)的符號定義為「0」。具體而言，例如在表27 中，若此陣列為a[x][y]，x 為1~10，代表請求項1~10；y 為0~9，其中的「0」代表該請求項之「多項狀態」，而之後的1~9 代表請求項之「依附關係」，亦即該請求項是否依附於項次在前的請求項；由於請求項只能依附於「項次在前」的請求項，故表27 之右上方是空白的，亦即，請求項1 不可能有依附項，請求項2 僅可能依附於請求項1，請求項3 僅可能依附於請求項1、2，而請求項10 則僅可能依附於請求項1~9。

因此，陣列a[1][0]、a[2][0]、a[3][0]、…、a[10][0]，代表請求項1~10 分別之「多項狀態」；陣列a[2][1]、a[3][1]、a[4][1]、…、a[10][1]，代表請求項2~10 分別是否有依附於請求項1；陣列a[3][2]、a[4][2]、a[5][2]、…、a[10][2]，代表請求項3~10 分別是否有依附於請求項2，依此類推。

接下來要說明第二個概念，也就是AI 修正程式之核心原理，表27中，黃色欄位若出現「1」值時，係如何對粉紅色欄位的「1」值造成影響？

如前所述，黃色欄位的「1」代表請求項為「多項附屬項」或是「直接或間接依附於多項附屬項之單項附屬項」，因此，黃色欄位值若為「0時」，則代表該請求項並非上述兩種情況，則剩下的情況為：該請求項為「獨立項」或是「並非直接或間接依附於多項附屬項之單項附屬項」。
以下，藉由表28 舉例說明黃色欄位若出現「1」值時，係如何對粉紅色欄位的「1」值造成影響。

＜表28：多依多修正AI 程式之陣列＞

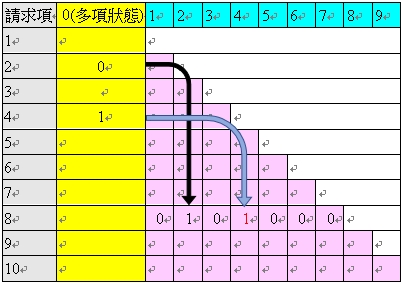
表28 中，第九列的請求項8 中，右方粉紅色欄位中的數字，由左到右為{0,1,0,1,0,0,0}，表示請求項8 係依附於請求項2 或4 項。其中，請求項2 的黃色欄位為「0」，表示請求項2 為「獨立項」或「(未間接依附到多項附屬項之)單項附屬項」；又，請求項4 的黃色欄位為「1」，表示請求項2 為「多項附屬項」或「間接依附到多項附屬項之單項附屬項」。
此時，由於請求項4 的黃色欄位為1，在請求項8 的粉紅色欄位中，對應到請求項4 的位置，我們將其數字「1」標示為紅色的數字「1」，以資區別。
因此，從表28 中，我們從請求項8 右邊粉紅色欄位的{0,1,0,1,0,0,0}理解到，請求項8 係依附於請求項2 或4 項，故請求項8 本身為一多項附屬項，又，由於請求項8 右邊粉紅色欄位的{0,1,0,1,0,0,0}中，左邊數來第四個位置出現了紅色的「1」，表示請求項4 亦為一「多項附屬項」或是「會間接依附到多項附屬項之單項附屬項」，因此，請求項8 依附於請求項4 時，會出現「多依多」之情事。
接下來，我們來看AI 程式如何去處理「多依多」之情形。
＜多依多的解除＞
要藉由「刪項修正」解決多依多的問題，至少有以下兩種方式：
1、第一種解除方式，是大家比較容易想到的，若一多項附屬項的依附對象中，存在其它多項附屬項(或是「會間接依附到多項附屬項之單項附屬項」)，則只要將這些依附對象刪除，即可解決多依多的問題。
2、第二種解除方式，要從另一個角度思考。
「多項」依附「多項」，前面的那個「多項」，表示本身是「多項附屬項」，而後面的那個「多項」，表示依附的對象中，存在其它的「多項附屬項」。
上述情事為多項附屬項間直接依附之情形。另外，在間接依附之情形，此時的「多項」依附「多項」，前面的那個「多項」，仍表示本身是「多項附屬項」，而後面的那個「多項」，表示依附的對象中，存在其它的「會間接依附到多項附屬項之單項附屬項」。

因此，要解決「多項」依附「多項」的問題，就要將前面的那個「多項」與後面的那個「多項」當中的其中一者處理掉。
上述的第一種解除方式，係將後面的那個「多項」處理掉，而變成「多項」依附「單項或獨立項」，而解決了多依多的問題。

說到此，相信各位已能輕易思及第二種解除方式，自然就是解決掉前面那個「多項」，而變成「單項」依附「多項」之情形，以解決多依多的問題(前面的那個「多項附屬項」的依附對象移除到剩下一項時，本身成為「單項附屬項」)。
＜多依多的第一種解除方式＞
如前所述，多依多的第一種解除方式，為刪除依附對象中所有「有問題」的(「多項狀態」為1 的)請求項，在AI 程式中，程式會將多項附屬項所依附到的請求項(1 或1)中，所有的(1)修正為(0)，亦即，刪除了「直接依附到的多項附屬項」或是，依附到的「會間接依附到多項附屬項的單項附屬項」。
以下，使用表29 舉例說明：

＜表29：多依多的第一種解除方式之說明＞

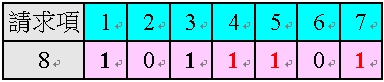
表29 中，請求項8 係依附於請求項1、3~5、7 中任一項，其中請求項4、5 及7 為「多項附屬項」或「會間接依附到多項附屬項的單項附屬項」，而有多依多之情形；在此，為解決表29 中多依多的情形，需從所依附到的請求項(1 或1)中，將所有的(1)修正為(0)，而成為以下表30 之情形：

＜表30：多依多以第一種解除方式修正後＞

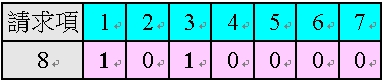
修正後的請求項8，係依附於請求項1 或3，其中請求項1 為獨立項，請求項3 應為一單項附屬項，故已解除了多依多之情形。
＜多依多的第二種解除方式＞
如前所述，多依多的第一種解除方式，係將請求項本身變成單項附屬項，也就是將依附的對象刪到僅保留一項。
以下，使用表31 舉例說明：

＜表31：多依多的第二種解除方式之說明＞

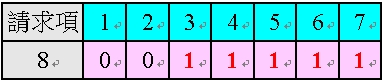
表31 中，請求項8 係依附於請求項3~7 中任一項，其中請求項3~7 均為「多項附屬項」或「會間接依附到多項附屬項的單項附屬項」，而有多依多之情形；在此，為解決表31 中多依多的情形，需將依附對象移除到剩下一項，而成為以下表32 之情形：

＜表32：多依多以第二種解除方式修正後＞

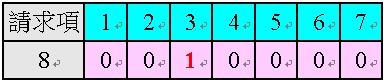
修正後的請求項8 係依附於請求項3，為一單項附屬項，故已解除了多依多之情形。
在此，欲將表31 的依附對象移除到剩下一項，自然不只上述表32 中留下請求項3 的方式，亦可留下請求項4~7 中任一項，然而，基於前述＜原則2＞，僅會選擇留下項次最為前面的請求項3。

＜多依多的「第一種解除方式」與「第二種解除方式」之判斷＞
以上介紹完AI 程式使用兩種不同的解除方式進行「刪項修正」之情形，但此AI 程式的修正模式是固定的，不會出現兩種方式都可進行的情形，因此，AI 程式亦藉由前述＜原則2＞，來判斷需啟動「第一種解除方式」與「第二種解除方式」中之哪一種模式。
具體而言，＜原則2＞規定應盡量保留依附對象中項次在前的請求項，對AI 程式而言，必然會去保留依附對象中，項次最為前面的請求項，並盡可能留下最多的依附對象，以使權力最大化。
因此，當粉紅色欄位從左邊數來第一個出現的1 為黑色的「1」時，由於第一個1 代表依附對象中項次最為前面的請求項，故此項必定要保留，此時，為了盡量使刪項後的權利範圍最大化，將採取「第一種解除方式」，將所有紅色的「1」刪除，如下表33 所示：

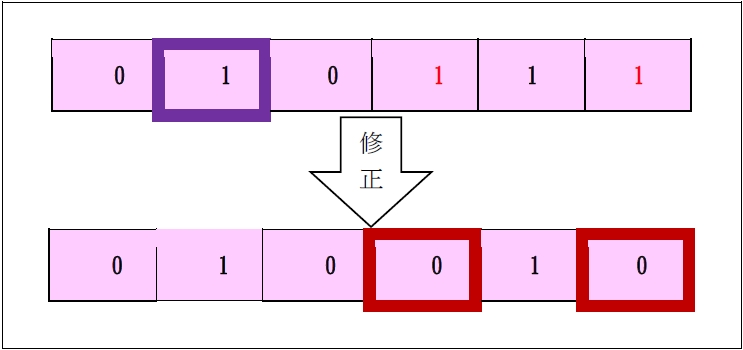
然而，當粉紅色欄位從左邊數來第一個出現的1 為紅色的「1」時，因為此項必定要保留，且若保留此項，將不能再保留任何其它依附對象，此時，將採取「第二種解除方式」，將所有其它的「1」及「1」刪除，僅保留第一個「1」，如下表34 所示：

＜表34：第一個1 為紅色的「1」時，刪除所有其它的「1」及「1」＞

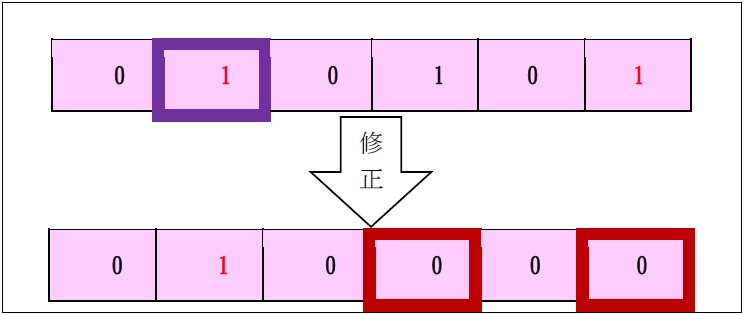
上述表33 及表34 的規則看似複雜，實則不然。當粉紅色欄位出現兩項以上的1 時，表示此請求項為一多項附屬項，需進行多依多之刪項修正；而前述「多依多」的刪項修正有兩種方式，「多依多」表示：「自身請求項為『多項附屬請求項』，且依附到的對象中，直接或間接地存在『多項附屬請求項』」，而兩種不同的刪項方式，分別是第一個方式處理掉依附到的對象中的「多項附屬請求項」以及「會間接依附到多項附屬項的單項附屬項」，或是第二個方式處理掉該請求項自身為「多項附屬請求項」之身份；通常情況下，為了盡量保留下較多的依附對象，AI 程式會採用第一個方式，僅刪除必要的依附對象而盡可能地留下最多的依附對象，然而，為了符合＜原則2＞，當依附對象中項次最大的請求項即為「多項附屬請求項」或是「會間接依附到多項附屬項的單項附屬項」時，AI 程式則會採用第一個方式，將該請求項本身變為單項附屬項，以克服多依多的問題。

＜AI 程式啟動粉紅色欄位需修正的邏輯＞
前面的段落剛介紹完若欲修正粉紅色欄位時，該如何修正？以下，將介紹何時會啟動修正粉紅色欄位？
首先，在進行多依多的修正時，需要處理的對象永遠只有請求項當中的「多項附屬項」，至於「單項附屬項」或是「獨立項」，則無需處理。
理由在於，如前所述，「多依多」表示：「自身請求項為『多項附屬請求項』，且依附到的對象中，直接或間接地存在『多項附屬請求項』」，因此，若自身請求項並非「多項附屬請求項」，自然不會發生「多依多」之情事，而無需處理。
接者，在對於請求項當中複數「多項附屬項」進行處理時，雖然對於第一項的(項次最前面的)「多項附屬項」進行處理，亦可避免後面的(項次較為後面的)「多項附屬項」依附回來時之「多依多」的情形發生，但是，基於＜原則1＞，我們並不會對於第一項的「多項附屬項」進行刪項處理。
事實上，第一項的「多項附屬項」，雖然做為「被依附的對象」時，會如前述般因後面的「多項附屬項」依附回來，而發生「多依多」的情形；然而，作為第一項的「多項附屬項」，其前面的請求項必定為「獨立項」或是「單項附屬項」(若非如此，亦即若前面還有其它的「多項附屬項」，則此項也不會成為第一項的「多項附屬項」)，因此，此第一項的「多項附屬項」本身在依附到項次更為前面的依附對象時，必然不會發生「多依多」之情
形。

綜上所述，AI 程式啟動粉紅色欄位的修正，需同時滿足以下兩項條件：

1、如果粉紅色欄位中有複數個1 存在(不論為紅色或黑色)，表示該請求項為一「多項附屬項」，可能需啟動修正。
2、對於第一項有複數個1 存在(不論為紅色或黑色)的請求項，亦即，對於第一項的「多項附屬項」，基於＜原則1＞，及其本身必無「多依多」之理由，無需啟動修正。
換言之，AI 程式啟動「粉紅色欄位的修正」之條件，在於其有複數個1，且不是第一個有複數個1、而是第二個以後有複數個1 之粉紅色欄位，亦即，係對於原請求項中，在多項附屬項中排序在第二項以後的多項附屬項，啟動修正。
在此需注意，啟動修正後，不代表對象請求項一定會被修正，若對象請求項雖為多項附屬項，但依附到的對象均為獨立項或無間接多項情形之單項附屬項，亦即有複數個1，但都是黑色的「1」之情形，此時，啟動修正後的結果，因為第一個「1」是黑色，會刪除所有紅色的「1」，但由於所有的1 都是黑色的「1」，所以修正後的結果，不會有任何改變。

＜AI 程式判斷黃色欄位應為「0」或「1」的邏輯＞
相較於粉紅色的欄位的修正不一定會啟動，所有的黃色欄位則是一定要進行判斷，以作為後面的請求項依附回來時是否需刪除依附對象之依據。
對於上一段落中所述需啟動粉紅色欄位的修正之請求項，需於修正完粉紅色欄位後，亦即對該請求項做完刪項後，再進行黃色欄位之判斷。
而若非需進行粉紅色欄位的修正之請求項，例如，獨立項、單項附屬項、或是第一項多項附屬項，因無修正必要，故可直接進行黃色欄位之判斷。
(1)、無需修正請求項之情況下，黃色欄位之值的判斷
下表35 說明各種無需修正請求項，亦即無需進行粉紅色欄位的修正之情況下，黃色欄位為「0」或「1」之值的判斷：

＜表35：各種無需修正的情況下，黃色欄位為「0」或「1」的判斷＞

NO.	情況	黃色欄位之值
1	獨立項	0
2	單項附屬項，粉紅色欄位為紅色的「1」	1
3	單項附屬項，粉紅色欄位為黑色的「1」	0
4	第一個多項附屬項，粉紅色欄位均為黑色的「1」	1

表35 中說明了四種無需修正的情況之黃色欄位值，包含：
情況1、由於該請求項為獨立項(粉紅色欄位不存在、或為複數個0)，故後項的多項附屬項依附回來時，不會產生多依多之情形，因此，其黃色欄位是「0」；

情況2、雖然該請求項為單項附屬項(粉紅色欄位為一個「1」)，但是其紅色的「1」代表後項的多項附屬項依附回來時，會產生「間接依附於多項附屬項」之情形，故其黃色欄位是「1」；
情況3、該請求項為單項附屬項(粉紅色欄位為一個「1」)，且其中的黑色的「1」代表後項的多項附屬項依附回來時，不會產生「間接依附於多項附屬項」之情形，故其黃色欄位是「0」；
情況4、該請求項為第一個多項附屬項(粉紅色欄位為複數個黑色的「1」)，因為是第一個多項附屬項，所以其本身無需修正粉紅色欄位(且都是黑色的「1」，故就算修正也不會改變)；由於該請求項為多項附屬項，故後項的多項附屬項依附回來時，會產生「直接依附於多項附屬項」之情形，因此，其黃色欄位是「1」。

(2)、進行完請求項之修正後，黃色欄位之值的判斷
以上，說明完各種無需修正請求項之情況下，黃色欄位之值的判斷，接下來，說明需先修正請求項，亦即需先修正完粉紅色欄位後，黃色欄位之值的判斷。
基本上，當需進行粉紅色欄位的修正時，只要記得，應以修正後的粉紅色欄位之狀況來判斷黃色欄位，而非修正前的。
其原因在於，若一請求項為多項附屬項，則後項的多項附屬項依附回來時，會「直接依附於多項附屬項」，而有多依多之情形；然而，若該請求項已進行過修正，刪減了依附對象，而從多項附屬項被修正成單項附屬項，且例如係依附於獨立項之單項附屬項，此時，後項的多項附屬項依附回來時，就不會產生多依多之情形。
因此，黃色欄位的判斷，的確應以請求項修正後之狀態為之，而非修正前之狀態。
下表36 說明各種進行過粉紅色欄位的修正之情況下，黃色欄位「0」或「1」之值的判斷：

＜表36：各種進行過修正的情況下，黃色欄位「0」或「1」的判斷＞

NO.	情況	黃色欄位之值
1	變為單項附屬項，但粉紅色欄位為紅色的「1」	1
2	變為單項附屬項，且粉紅色欄位為黑色的「1」	0
3	仍為多項附屬項，粉紅色欄位均為黑色的「1」	1

表36 中黃色欄位的判斷邏輯基本上與表35 中相同，故省去詳細的說明。表36 的情況1，第二個以後的多項附屬項在被修正後，雖然變成了單項附屬項，但仍可能造成後項的「間接多依多」，故黃色欄位為「1」；情況2，修正後變成了單項附屬項，且後項不會有「間接多依多」的可能，故黃色欄位為「0」；情況3，修正後仍為多項附屬項，故後項會有「直接多依多的可能」，故黃色欄位為「1」。

表36 的情況不複雜，只要記得需先進行完粉紅色欄位的修正，再來進行黃色欄位的判斷即可。

＜AI 程式數值變化Demo＞
以上，已說明完AI 程式的各種運作原理，但在實際進行案例演練之前，相信各位讀者應該還是會覺得有些不解與困惑。
接下來，讓我們用一實際案例說明AI 程式如何判斷請求項中多依多的問題，並提出修正建議。
首先，以下的表37 為一個做為處理對象之請求項：

＜表37：處理對象之請求項＞
1、一種OO…。
2、如請求項1 之OO，其中…。
3、如請求項1 或2 之OO，其中…。
4、如請求項3 之OO，其中…。
5、如請求項2 至4 中任一項之OO，其中…。
6、如請求項2 至5 中任一項之OO，其中…。
7、如請求項3 至6 中任一項之OO，其中…。
8、如請求項3 至7 中任一項之OO，其中…。
9、如請求項8 中任一項之OO，其中…。
10、如請求項1 之OO，其中…。

表37 的請求項共計10 項，其中第1 項為獨立項，第2~10 項為第1 項之直接或間接的附屬項。
在此，將表37 的依附關係整理為以下精簡的依附關係表38：

＜表38：處理對象之請求項的依附關係＞

請求項	1	2	3	4	5	6	7	8	9	10
依附關係	獨立項	1	1,2	3	2~4	2~5	3~6	3~7	8	1

表38 中，我們知道請求項1 為獨立項，請求項2 依附於請求項1，請求項3 依附於請求項1 或2…。正如表37 中所示。
接下來，我們將表38 中各請求項初始依附關係填入AI 程式的陣列中，而得到以下的表39：

＜表39：填入「初始依附關係後」的多依多修正AI 程式之陣列＞

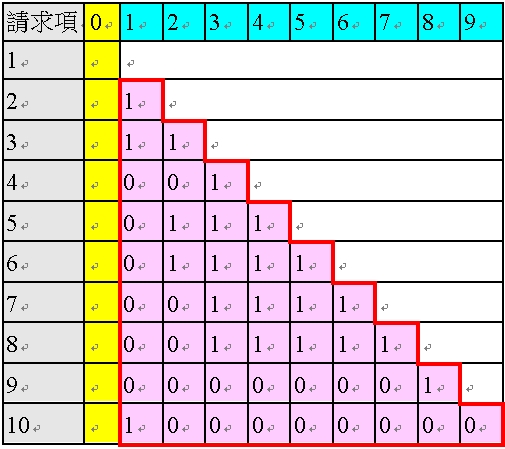
從表39 可看到AI 程式將使用者輸入的「各請求項初始依附關係」讀入後的狀態。
接下來，AI 程式將逐項檢示各請求項的粉紅色欄位是否需修正，並於黃色欄位填上各請求項的「多項狀態」。
首先，關於請求項1 的黃色欄位，AI 程式會先判斷請求項1 為何種請求項，當然，我們都知道，請求項1 既為第一個請求項，其前面沒有其它請求項可以依附，自然是獨立項；然而，對AI 程式而言，判斷獨立項的方式為，當粉紅色欄位裡面的值全部為「0」，也就是其沒有依附到項次在前的任何請求項的時候，判斷該請求項為獨立項，並在其黃色欄位填入「0」；或是，當該請求項不存在粉紅色欄位的情形(該請求項不存在項次在前之請求項)，也就是第一項的請求項(請求項1)的情形，亦會判斷該請求項為獨立項，並在其黃色欄位填入「0」。
因此，AI 程式在分析完請求項1 不存在粉紅色欄位後，便會基於表35 之情況1，判斷出應於請求項1 之黃色欄位填上「0」，如以下的表40：

＜表40：填入「請求項1 的黃色欄位」後的多依多修正AI 程式之陣列＞

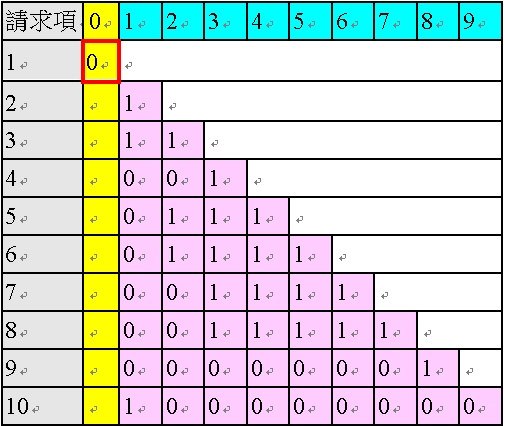
接下來，關於請求項2，由於其粉紅色欄位中只有一個「1」，為單項附屬項，故其無需進行粉紅色欄位的修正，可直接進行黃色欄位的判斷。基於表35 之情況3，由於請求項2 僅有一個1為單項附屬項，且為黑色的「1」，故AI 程式判斷其黃色欄位為「0」，如以下之表41。

＜表41：填入「請求項2 的黃色欄位」後的多依多修正AI 程式之陣列＞

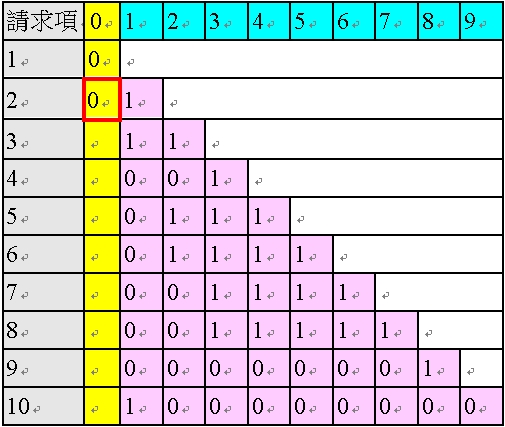
接下來，關於請求項3，由於其粉紅色欄位中有兩個「1」，為多項附屬項，乍看之下需先進行修正，再判斷其黃色欄位。然而，基於表35 之情況4，由於請求項3 為第一個多項附屬項，自然，其粉紅色欄位均為黑色的「1」，故其實是無需修正，AI 程式基於其粉紅色欄位有複數個「1」為多項附屬項，而判斷其黃色欄位為「1」，如以下之表42(在此，就算對請求項3 的粉紅色欄位先進行修正，因其第一個1 為黑色的「1」，將採取表33 的「第一種解除方式」，將所有紅色的「1」刪除，但請求項3 的粉紅色欄位只有兩個黑色的「1」，沒有紅色的「1」，故修正後也不會改變；因此，亦可不判斷是不是第一項多項附屬項，而對於所有多項附屬項均啟動修正程式)。

＜表42：填入「請求項3 的黃色欄位」後的多依多修正AI 程式之陣列＞

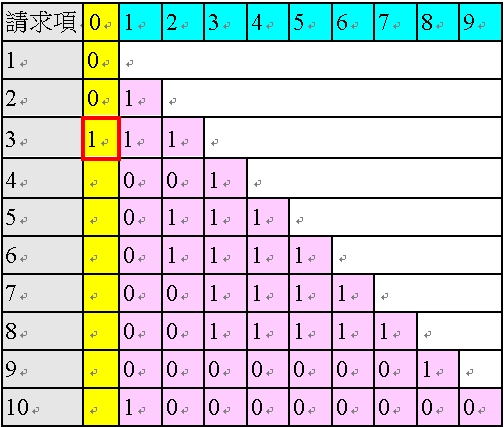
在此，於表42 中，黃色欄位出現了第一個「1」，在表28 中，我們介紹過黃色欄位的「1」係如何影響項次在後的請求項的粉紅色的欄位中的「1」。具體而言，由於請求項3 的黃色欄位為1，將造成項次在後的請求項之粉紅色欄位中對應於請求項3 的部分的黑色的「1」，變成紅色的「1」(筆者將此機制稱為「感染」或「連鎖破壞」)，如以下表43 所示：

＜表43：請求項3 黃色欄位的「1」對後項造成「感染」＞

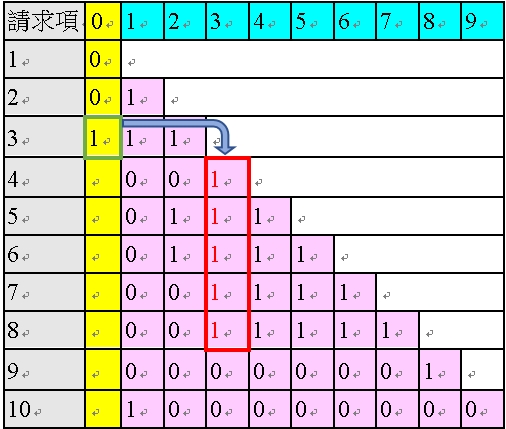
接下來進入請求項4，請求項4 的粉紅色欄位中只有一個1，為單項附屬項，故無需進行粉紅色欄位的修正，可直接進行黃色欄位的判斷。基於表35 之情況2，由於請求項4 僅有一個1，為單項附屬項，但為紅色的「1」(後項依附回來時會造成間接多依多)，故AI 程式判斷其黃色欄位為「1」，如以下之表44。

＜表44：填入「請求項4 的黃色欄位」後的多依多修正AI 程式之陣列＞

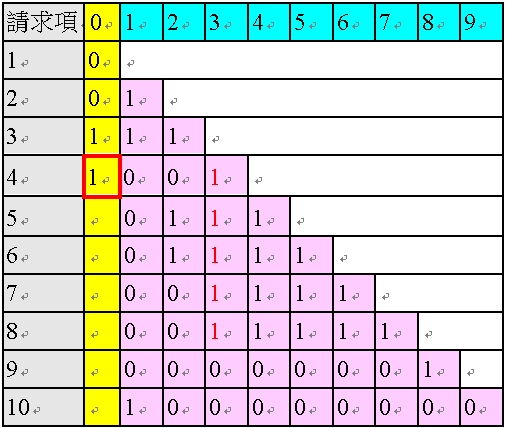
在此，於表44 中，黃色欄位又出現了一個「1」，與表43 的情形相同，由於請求項4 的黃色欄位為1，將造成項次在後的請求項之粉紅色欄位中對應於請求項4 的部分的黑色的「1」，變成紅色的「1」，如以下表45 所示：

＜表45：請求項4 黃色欄位的「1」對後項造成「感染」＞

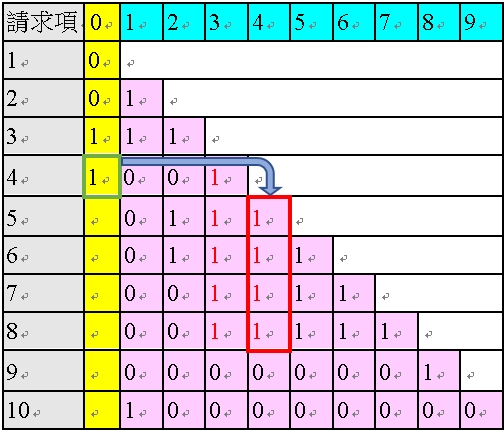
接下來進入請求項5，因請求項5 的粉紅色欄位中有三個1，為多項附屬項，故需進行粉紅色欄位的修正。由於粉紅色欄位中的第一個1 為黑色的「1」，基於表33 的「第一種解除方式」，刪除所有紅色的「1」，如以下表46 所示：

＜表46：對請求項5 的粉紅色欄位修正後的多依多修正AI 程式之陣列＞

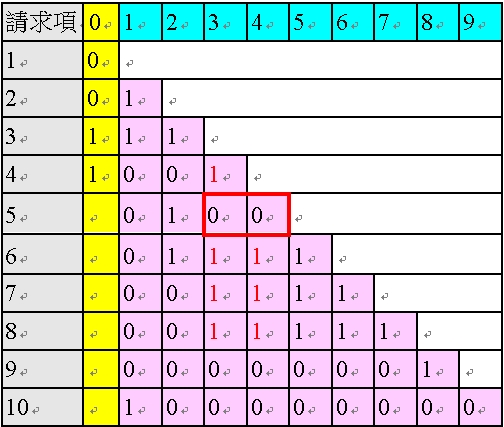
進行完請求項5 的粉紅色欄位的修正後，基於修正後的粉紅色欄位，進行請求項5 的黃色欄位的判斷。
由於請求項5 修正後僅剩下一個1，為單項附屬項，且為黑色的「1」(類似上述無需修正之請求項2 的情形)，故AI 程式基於表36 之情況2，判斷其黃色欄位為「0」，如以下之表47。

＜表47：填入「請求項5 的黃色欄位」後的多依多修正AI 程式之陣列＞

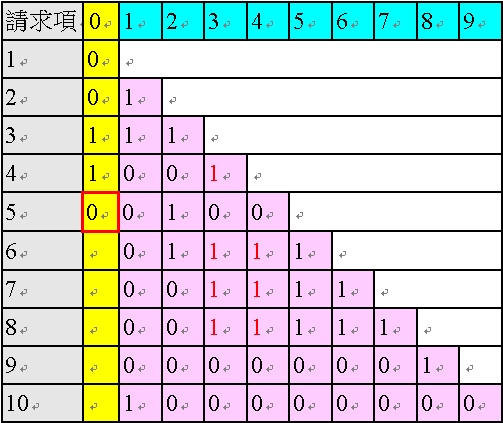
接下來進入請求項6，請求項6 的粉紅色欄位中有四個1，為多項附屬項，需進行粉紅色欄位的修正。由於粉紅色欄位中的第一個1 為黑色的「1」，基於表33 的「第一種解除方式」，刪除所有紅色的「1」，如以下表48 所示：

＜表48：對請求項6 的粉紅色欄位修正後的多依多修正AI 程式之陣列＞

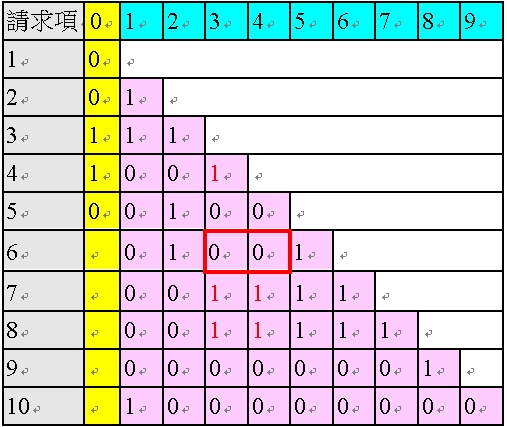
進行完請求項6 的粉紅色欄位的修正後，基於修正後的粉紅色欄位，進行請求項6 的黃色欄位的判斷。
由於請求項6 修正後剩下兩個1，為多項附屬項(類似上述無需修正之請求項3 的情形)，故AI 程式基於表36 之情況3，判斷其黃色欄位為「1」，如以下之表49。

＜表49：填入「請求項6 的黃色欄位」後的多依多修正AI 程式之陣列＞

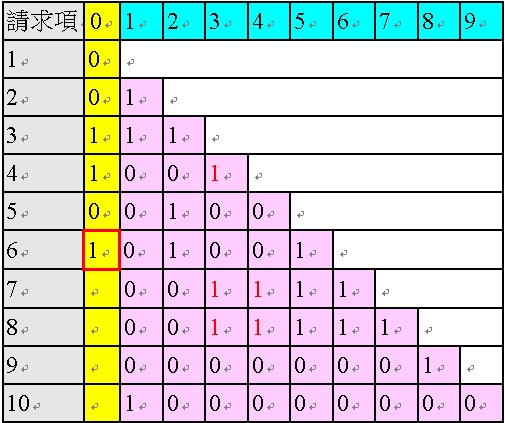
接下來進入請求項7，請求項7 的粉紅色欄位中有四個1，為多項附屬項，需進行粉紅色欄位的修正。由於粉紅色欄位中的第一個1 為紅色的「1」，基於表34 的「第二種解除方式」，僅留下第一個紅色的「1」，如以下表50 所示：

＜表50：對請求項7 的粉紅色欄位修正後的多依多修正AI 程式之陣列＞

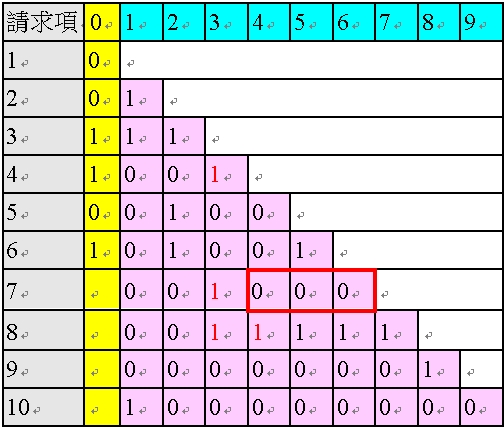
進行完請求項7 的粉紅色欄位的修正後，基於修正後的粉紅色欄位，進行請求項7 的黃色欄位的判斷。
由於請求項7 修正後僅剩一個1，但為紅色的「1」(後項依附回來時會造成間接多依多)，故AI 程式基於表36 之情況1，判斷其黃色欄位為「1」，如以下之表51。

＜表51：填入「請求項7 的黃色欄位」後的多依多修正AI 程式之陣列＞

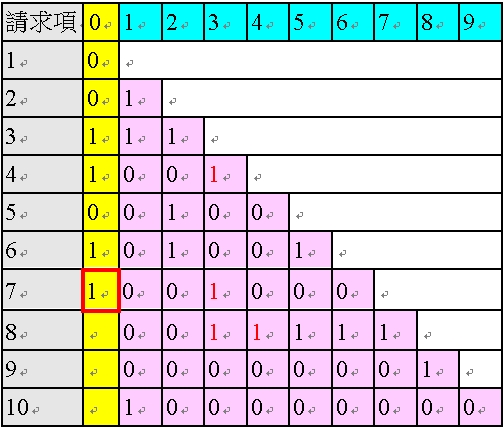
在此，於表51 中，由於請求項7 的黃色欄位為1，將造成項次在後的請求項之粉紅色欄位中對應於請求項7 的部分的黑色的「1」，變成紅色的「1」，如以下表52 所示：

＜表52：請求項7 黃色欄位的「1」對後項造成「感染」＞

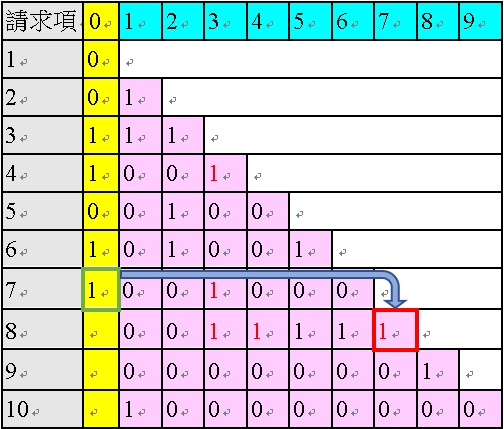
接下來進入請求項8，請求項8 的粉紅色欄位中有五個1，為多項附屬項，需進行粉紅色欄位的修正。由於粉紅色欄位中的第一個1 為紅色的「1」，基於表34 的「第二種解除方式」，僅留下第一個紅色的「1」，如以下表53 所示：

＜表53：對請求項8 的粉紅色欄位修正後的多依多修正AI 程式之陣列＞

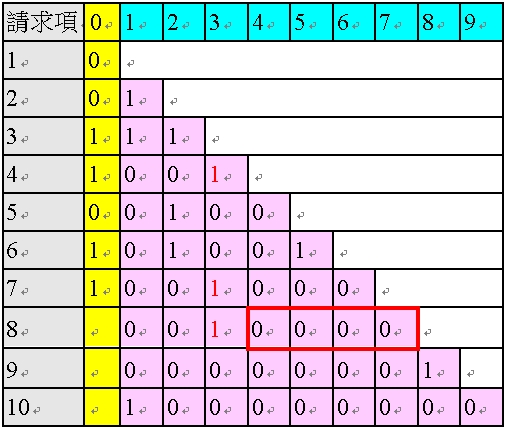
進行完請求項8 的粉紅色欄位的修正後，照理而言，接下來，應該繼續進行請求項8 黃色欄位判斷、對於後方請求項9 粉紅色欄位的感染，接著，是請求項9 及10 的粉紅色欄位修正確認、黃色欄位判斷、感染等，然而，由於請求項9、10 的粉紅色欄位中各自均只有一個「1」，均為單項附屬項，不會有「多依多」之情形，換言之，進行完最後一項的「多項附屬項」、也就是請求項8 的粉紅色欄位的修正後，AI 程式將會自動脫離迴圈，輸出
修正結果如以下表54：

＜表54：修正後的處理對象之請求項的依附關係＞

請求項	1	2	3	4	5	6	7	8	9	10
依附關係	獨立項	1	1,2	3	2	2,5	3	3	8	1

將表54 還原為文字版的請求項，如以下表55：

＜表55：修正後的處理對象之請求項＞

1、一種OO…。
2、如請求項1 之OO，其中…。
3、如請求項1 或2 之OO，其中…。
4、如請求項3 之OO，其中…。
5、如請求項2 之OO，其中…。
6、如請求項2 或5 之OO，其中…。
7、如請求項3 之OO，其中…。
8、如請求項3 之OO，其中…。
9、如請求項8 中任一項之OO，其中…。
10、如請求項1 之OO，其中…。

＜AI 程式介面展示＞
最後，讓我們實際看一下筆者設計的AI 程式之使用介面：

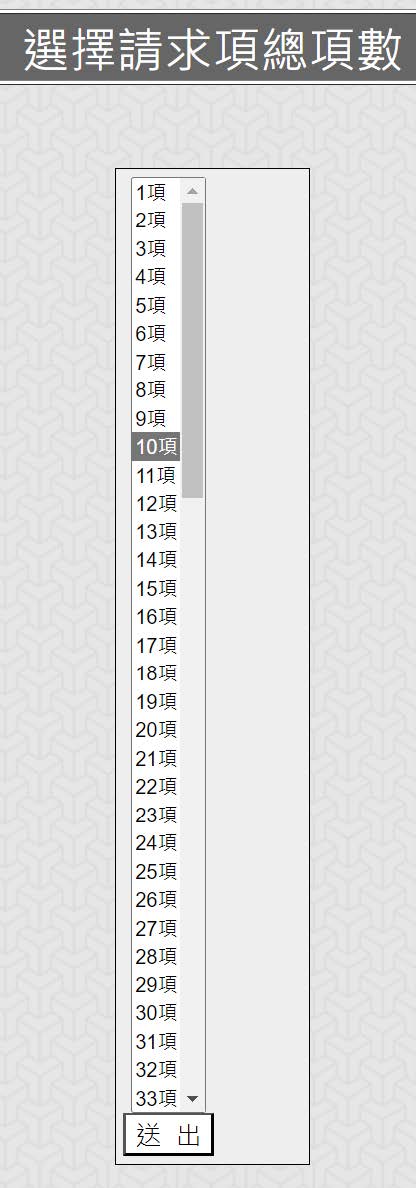
步驟1-設定請求項之總項數(下圖2)：
＜圖2：使用AI 程式之第一步驟-選擇請求項之總項數＞

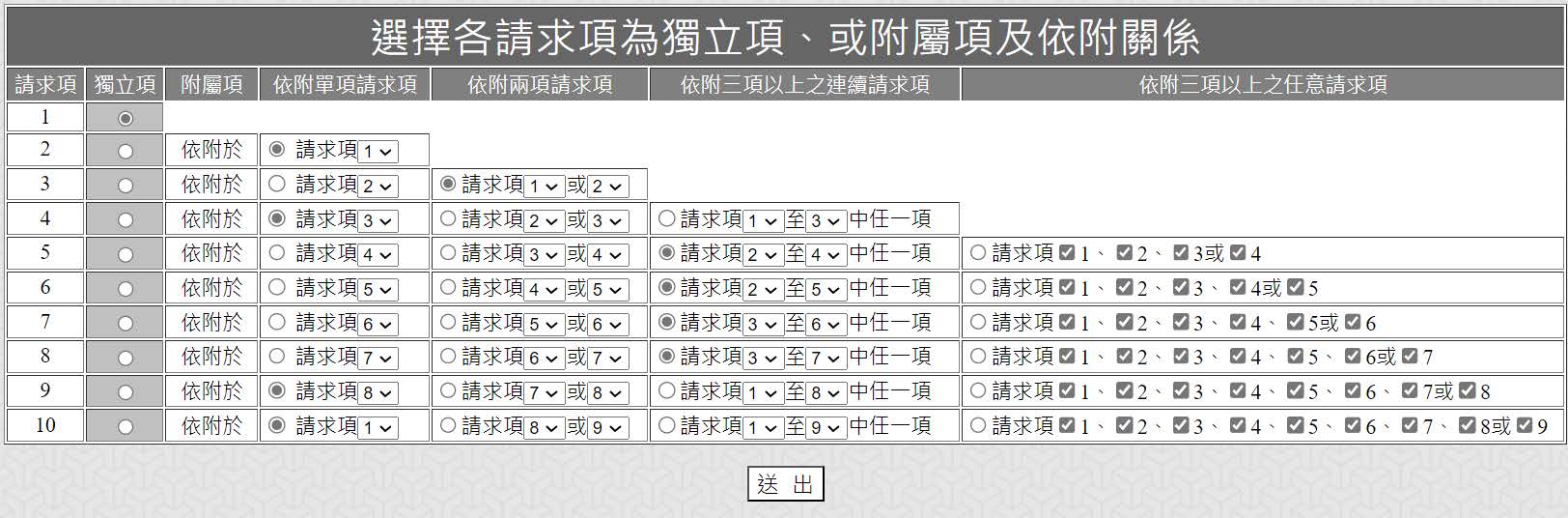
步驟2-設定各請求項之依附關係(下圖3)：

＜圖3：使用AI 程式之第二步驟-設定各請求項之依附關係＞

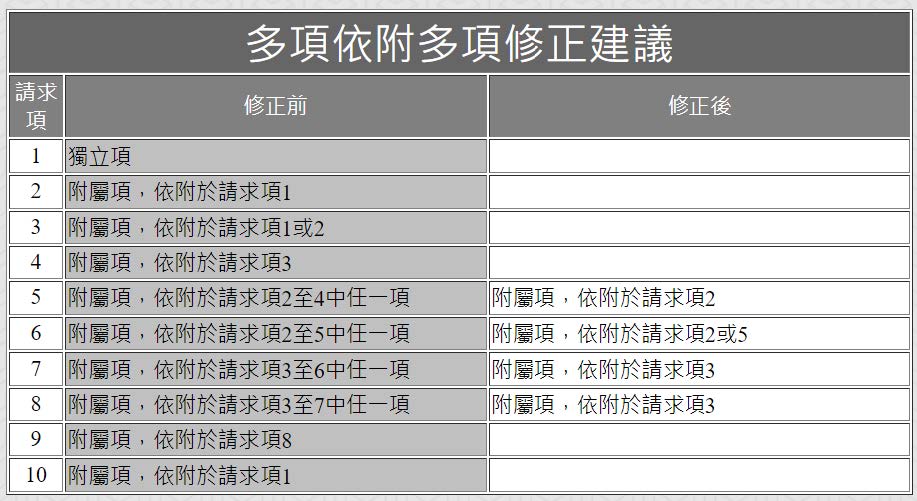
步驟3-AI 程式自動輸出「多依多修正建議」(下圖4)：
＜圖4：AI 程式輸出結果＞

以上，筆者首先比較了各大專利局對於「多項附屬項間直接或間接依附」之規定的異同，進而，說明了「多項附屬項間直接或間接依附之修正建議AI 程式」之開發動機。
在介紹此AI 程式前，筆者先說明「多項附屬項間『直接』或『間接』依附之情形」，並介紹了第一種多項附屬項間直接或間接依附時之修正方式，也就是「拆項修正」。
關於「拆項修正」，筆者解釋了對於「依附關係最大化(每一個附屬項都依附於前面所有請求項)之情形」，應如何進行拆項修正，方可使修正後之總項數最少？此外，筆者也推導了「依附關係最大化」之情況下，「拆項修正後之總項數」，係如何隨原總項數之增加而呈指數增長？
接著，筆者導入了多依多的第二種修正方式亦即「刪項修正」，並說明了筆者定義的兩個「刪項修正」時的原則：
＜原則1＞選擇「項次較後面的請求項」進行「刪項」修正。

＜原則2＞刪除所依附的項次中「項次較後面者」。
最後，筆者開始介紹自行研發的「多依多之修正建議AI 程式」。從其設計原理，包含代表「多項狀態」之黃色欄位及代表「依附關係」之粉紅色欄位，到多依多刪項修正的「第一種解除方式」及「第二種解除方式」，乃至於「需啟動粉紅色欄位修正的邏輯」。接著，透過AI 程式數值變化的實際Demo，我們看到AI陣列中黃色欄位中的「1」，對於粉紅色欄位中的黑色的「1」進行感染，使其成為紅色的「1」等現象，並完成請求項的多依多刪項修正。
同時，筆者也展示程式的使用介面及輸出結果畫面。
透過本文揭露的內容，相信能使讀者對於多依多修正及利用AI 程式輔助多依多修正之判斷技術，能有更深一層的理解。
若對於本文揭露的內容認為有不合理之處，或有任何疑惑想與筆者討論，均歡迎透過本所官網進行留言，來信與筆者討論。

在專利侵權訴訟中，專利權人須舉證被控侵權人在未經其同意下實施其專利，且主觀上有故意或過失，以爭取損害賠償。然而，當專利侵權訴訟涉及承攬契約時，定作人往往不會涉及實施專利的行為，而承攬人同時會抗辯其僅為按圖施作，並無侵害專利權之故意或過失，使專利侵權訴訟中的責任歸屬趨於複雜。因此，本文從專利權的效力及專利侵權損害賠償的構成要件出發，探討承攬制度中可能發生的爭訟狀況，並以我國實際判例探詢智財法院的裁判立場。
關鍵字：專利侵權、損害賠償、實施、承攬、按圖施作、故意、過失
Patent Infringement、Compensation、Exploitation、Contract、Construct-todrawing、Intentional Act、Negligence

我國的營造、建築工程經常涉及多人分工的承攬制度，其中承攬人在承包定作人的工程後，可能會繼續將該工程細分並發包給一或更多次承攬人。此時，若該工程涉及專利侵權訴訟，除了專利權人可能無法明確界定請求損害賠償的對象（即，民事訴訟當事人的適格性）之外，定作人與承攬人之間的責任分屬也是影響損害賠償成立與否的重大因素。
另外，我國於2020 年11 月1 日起正式施行設計專利實體審查基準修正案，明定建築物及室內設計（亦統稱為「建築工程設計」）得為設計專利的保護標的，使我國設計專利的保護範圍大幅擴展。隨著與建築工程相關的專利規模逐漸擴大，相關的專利侵權訴訟數量也會隨之增加。因此，承攬制度對於專利侵權訴訟所產生的影響，確實是一個值得討論的議題。因此，筆者欲以實際法院判決來探討，當專利侵權訴訟涉及承攬契約時法院的立場及裁判的方向為何，並期望以本文作為借鑒，使定作人與承攬人能理解其各自在承攬契約中分別具有何種程度的專利權注意義務，以提升相關業者的智慧財產權意識。

一、專利權效力及專利實施
根據我國專利法第58 條第1 項規定：「發明專利權人，除本法另有規定外，專有排除他人未經其同意而實施該發明之權」，其中，前述實施包含物之發明的實施，以及方法發明的實施。物之發明之實施，指「製造、為販賣之要約、販賣、使用或為上述目的而進口該物之行為」；而方法發明之實施，指「使用該方法；或是使用、為販賣之要約、販賣或為上述目的而進口該方法直接製成之物」，分別於我國專利法第58 條第2 項及第3 項定有明文。
換言之，在專利權範圍內，專利權人對於他人「實施」其所屬之發明具有一定程度的限制，而「實施」的具體態樣則定於專利法第58 條第2 項及第3 項中所表列的行為。若他人未經專利權人同意即任意進行上述行為，則可能會構成專利權侵害。
二、專利侵權損害賠償之構成要件
根據我國專利法第96 條第1 項規定：「發明專利權人對於侵害其專利權者，得請求除去之。有侵害之虞者，得請求防止之」；而同法第96 條第2 項規定：「發明專利權人對於因故意或過失侵害其專利權者，得請求損害賠償」（新型及設計專利準用）。據此，若專利權人欲對於侵害其專利權者（被控侵權人）請求損害賠償，必須證明被控侵權人對於侵權行為有主觀上的「故意或過失」。
因此，根據我國專利法之敘述，可將專利侵權損害賠償之構成要件分成二個要件：第一，被控侵權人在未經專利權人的同意下進行專利法第58 條所規定的實施態樣；第二，被控侵權人對於侵權行為需有主觀上的故意或過失，若缺乏任一要件，則專利侵權的損害賠償應無法成立。

實務上，針對前述二個條件進行抗辯是專利侵權訴訟的被告所常用的抗辯理由，即抗辯無實施行為或無侵權之故意或過失。通常，當專利侵權訴訟涉及單一被告時，專利權人不太可能在被告未實施其專利的情況下貿然提起訴訟，且必然會主張被告有侵權之故意或過失，以請求損害賠償。然而，若專利侵權訴訟涉及多人分工（例如，定作人與承攬人、製造商與零售商等）的情況，有時被告會分別主張無實施行為及無侵權之故意或過失的抗辯理由，即俗稱的「踢皮球」行為，此時理論上可能會發生「一被告無實施專利行為，另一被告無侵權之故意或過失」的情況，使該等被告均得以免除損害賠償責任。

我國民法第490 條規定：「稱承攬者，謂當事人約定，一方為他方完成一定之工作，他方俟工作完成，給付報酬之契約。」承攬制度與僱傭制度最大的差異在於定作人與承攬人之間並無從屬關係，因此承攬人在工作上能具有高度獨立性或主導權。承攬制度的常見案例為建案業主與營造商、建築設計事務所與施作工班，甚至可能是ㄧ般民眾與裝潢業者。承攬契約中的工作分配通常能簡單區分成以下二種情況：第一，定作人可能會在承攬契約中檢附詳細的物品或工程圖說，並給予相當的指示，而承攬人僅負責按圖施作；或者，定作人亦可能僅概略指定成品之製作，而設計細節由承攬人決定。在前者情況中，定作人無實施專利之行為，而承攬人也僅單純按圖施作，若該工程圖說中的設計涉及侵害他人專利權而專利權人欲請求損害賠償時，定作人是否會構成專利侵權損害賠償之構成要件中的「實施」要件，以及承攬人是否會構成「侵權之故意或過失」要件，將會是損害賠償是否成立的重點。而在後者的情況下，定作人在承攬契約期間無指示行為的情況下是否會涉及「共同侵權」，同樣會大幅度影響專利侵權訴訟中的損害賠償責任。

如前所述，由於我國於2020 年間開放建築工程設計可作為設計專利的申請標的，而建築工程經常涉及多人分工的承攬制度，因此與承攬契約相關的專利侵權訴訟數量可能也會隨著設計專利範圍的擴展而增加。然而，設計專利從撰寫至核准需要相當的時間，且專利侵權訴訟的期程往往十分漫長，因此目前尚未出現與承攬契約相關的設計專利侵權訴訟。於是，筆者以「承攬」、「實施」及「故意或過失」檢索近十年來的專利侵權訴訟判決，試圖以現有涉及承攬契約的判決來探詢智財法院過往的裁判立場，也能稍微了解未來若出現與承攬契約相關的設計專利侵權訴訟時，法院判決的趨勢可能為何。然而，筆者在檢索後發現，雖然許多案例符合「定作人以無實施專利之行為」且「承攬人以僅單純按圖施作而無侵權之故意過失」作為抗辯理由，但絕大多數的專利侵權訴訟往往伴隨「是否落入專利範圍」或「專利有效性」的爭點，一旦法院認為「未落入專利範圍」或「專利無效」即可作出判決，即不會對於「定作人有無實施專利之行為」或「承攬人以僅單純按圖施作是否即無侵權之故意過失」進行探討。儘管如此，筆者仍從中篩選出三件案情略有不同，但符合「定作人以無實施專利之行為」或「承攬人以僅單純按圖施作而無侵權之故意過失」作為抗辯理由的智財法院判決進行分析，期望探詢法院對於涉及承攬契約的專利侵權訴訟的立場。另外，由於本文是聚焦在專利侵權的「實施」及「侵權之故意或過失」的構成要件，故下列判例中的抗辯理由均省略關於「專利有效性」及「是否落入專利範圍」的論述，以免使焦點模糊。

一、智慧財產法院100 年度民專訴字第74 號判決
（一）案情簡介
本案（下稱第74 號判決）原告為新型第M296281 號及M297983 專利（下稱系爭專利）之專利權人。被告新北市政府之「孝恩堂納骨櫃增設工程」（下稱系爭工程）由被告利昌公司承攬施作，而利昌公司再將系爭工程轉包予被告大真武公司實際進行施作。
1. 原告主張
原告主張，被告所製造且販賣之骨灰甕收藏箱與其絞鏈結構（下稱系爭收納箱）已侵害其專利權，且被告於接獲原告之存證信函後仍繼續製造、販賣系爭收納箱，顯有侵害專利權之故意，應負損害賠償責任。
2. 被告抗辯
被告新北市政府略以「系爭工程之契約圖說中並無系爭專利之技術特徵，且其並未對系爭收納箱之設計另為指示。因此，縱使系爭收納箱落入系爭專利權範圍，應由承包廠商負完全責任，被告新北市政府無侵權之故意或過失可言」之理由進行抗辯。
被告利昌公司略以「系爭工程之製作部分已全數交由被告大真武公司施作，且施工圖及實際成品已由業主（被告新北市政府）核准通過，故已盡善良管理人之注意義務，無侵害專利權之故意或過失可言」之理由進行抗辯。
被告大真武公司則略以「其所製造之系爭收納箱均係依契約圖說進行施作，無侵權之故意或過失可言」之理由進行抗辯。
（二）法院裁判
關於被告新北市政府，法院認為根據民法第189 條之規定：「承攬人因執行承攬事項，不法侵害他人之權利者，定作人不負損害賠償責任。但定作人於定作或指示有過失者，不在此限」。被告新北市政府於系爭工程中有委任訴外人朱容兩建築師進行設計、監造等業務，故其僅為定作人，而非設計者或監造者。另外，系爭工程中是由訴外人朱容兩與被告大真武公司討論工程細節，被告新北市政府並未對被告利昌公司或大真武公司有任何指示，故難認定被告新北市政府於系爭收納箱的製造部份有侵害系爭專利權之故意或過失可言。
關於被告利昌公司，法院認為雖被告利昌公司辯稱系爭收納箱是由被告大真武公司施作，但訴外人朱容兩證稱系爭工程剛開始執行時是由被告利昌公司與其溝通，直到後期才由被告大真武公司之負責人員進行交涉。因此，被告利昌公司有參與系爭收納箱之施作細節討論的事實，故有查證系爭收納箱是否侵害他人專利權之義務，應負過失侵權責任。
關於被告大真武公司，雖其辯稱系爭收納箱是依照採購契約圖說進行施作，但訴外人朱容兩證稱被告大真武公司之負責人員有與其進行設計細節的溝通，且系爭工程之契約圖說中並無與系爭專利有關之技術特徵的構造。因此，被告大真武公司應負過失侵權責任。
（三）判例評析
本案屬於前述「定作人僅概略指定成品之製作，而設計細節由承攬人決定」的情況，而此情況的重點在於，定作人在承攬契約期間無指示行為是否仍會涉及「共同侵權」。

1. 定作人的共同侵權責任
對於被告新北市政府所述：「其未對承攬人及次承攬人下達任何指示，故無侵權之故意或過失，縱使系爭收納箱落入系爭專利權範圍，應由承包廠商負完全責任」之抗辯理由，本案原告在「對於被告抗辯所為之陳述」中援引民法第185 條第1 項，認為被告新北市政府身為業主，在已委託訴外人朱容兩建築師作為監造單位的情況下，並未履行監造、查驗承包廠商對於系爭收納箱之製造、販賣的義務，而此為造成侵害系爭專利權之共同原因，故應負共同侵權責任。
我國民法第185 條第1 項明定「數人共同不法侵害他人之權利者，連帶負損害賠償責任。不能知其中孰為加害人者亦同」，此為共同侵權之規定；而依據民法第189條之規定：「承攬人因執行承攬事項，不法侵害他人之權利者，定作人不負損害賠償責任。但定作人於定作或指示有過失者，不在此限」。因此，定作人須於定作或指示有過失時才需要負擔損害賠償責任。在本判決中，原告雖認為被告新北市政府涉及民法第185 條第1 項的共同侵權行為，但卻無法證明其在系爭工程的定作上有任何過失，亦無法證明其對於被告利昌公司或被告大真武公司有下達任何指示。因此，法院依民法第189 條之規定認為被告新北市政府無侵權之故意或過失而免除其損害賠償責任，於法有據。

2. 「討論」設計內容構成間接製造侵權？
本案被告利昌公司將系爭工程轉包給被告大真武公司實際進行施作，本身並無施作行為（即，製造專利物）。若依照前述專利侵權損害賠償的構成要件，被控侵權人必須涉及「實施」專利的行為，且對於侵權行為有主觀上的「故意或過失」。本案被告利昌公司於系爭工程期間僅涉及「討論」施作細節而未實際進行施作，但「討論」並不屬於我國專利法第58 條所規定的實施態樣，卻依然成立過失侵害專利權的原因為何，可能要參照我國民法第185 條。
如前所述，我國民法第185 條第1 項規定「數人共同不法侵害他人之權利者，連帶負損害賠償責任。不能知其中孰為加害人者亦同」。在學說上，共同侵權行為的類型涉及共同加害行為、共同危險行為及造意與幫助行為；其中，共同加害行為又分為主觀加害行為及客觀加害行為。所謂客觀加害行為，指數人縱無意思聯絡，各加害行為仍致生同一損害者而言。

從客觀加害行為的觀點來看，被告利昌公司作為系爭工程的承攬人，對於工作內容應具有高度獨立性或主導權，而具有查證次承攬廠商的行為是否涉及侵害他人專利權之義務。然而，被告利昌公司在系爭工程施作期間雖不涉及專利法第58 條所規定的實施行為，但也未履行適度的專利檢索義務或是監督次承攬人進行專利檢索，而間接導致侵權行為的發生。因此，筆者認為，被告利昌公司構成侵權行為的重點並非僅在於參與系爭收納箱之施作細節討論，還涉及身為系爭工程的承攬人，卻未履行主導該工程所伴隨的專利權注意義務而間接導致該製造侵權行為的發生。

另外，我國專利法僅明定直接侵權的態樣，即專利法第58 條之規定，並無間接侵權之規定。然而，在實務上與多人分工有關的專利侵權訴訟中經常涉及間接侵權的態樣（例如，本案被告利昌公司的情況），在專利法未明定間接侵權的情況下就必須回到民法進行論述。此做法的缺點在於，目前專利權人以民法規定提起訴訟的案件甚少，多數仍以專利法之規定起訴；然而，專利法僅明定直接侵權的態樣，如此便給予被告以「無涉及專利法第58 條所規定的實施行為」作為抗辯理由的機會，使訴訟情況變得相對複雜而可能減損專利權人的權益。因此，若未來專利法修訂時能引進民法關於間接侵權之規定，甚至參照他國專利法關於間接侵權的規定，相信能讓我國專利制度更加健全。

二、智慧財產法院108 年度民專訴字第12 號判決
（一）案情簡介
本案（下稱第12 號判決）原告佳埼鋼品有限公司為新型第M372866 號「樓層板複合結構」專利（下稱系爭專利）之專利權人。被告友達公司承攬臺東縣政府公開招標之「綠島觀光門戶設施尼伯特颱風災後復建工程」（下稱系爭工程），並且向被告杰逸公司購買施作該系爭工程所需之材料。
1. 原告主張
原告主張系爭工程已落入系爭專利之專利範圍內，且認為被告友達公司及被告杰逸公司均為相關同業，在承攬工程之前應施以相當注意，但卻疏於進行專利檢索侵害專利權人之專利權，故應負過失賠償責任。

2. 被告抗辯
被告友達公司略以「其與臺東縣政府就系爭工程簽訂工程契約，依約須履行該契約圖說所要求之規定，倘未依圖說施作，將有可歸責之債務不履行事由。另外，依政府採購法第26 條第3 項規定招標文件原則上不得要求使用專利，故自得合理認定該工程契約中的文件不會涉及他人專利。因此，被告友達公司無侵害系爭專利權之故意或過失可言」之理由進行抗辯。
被告杰逸公司則略以「在系爭工程期間僅轉售所需材料予友達公司，本身並無製造材料或施作工程之行為，主觀上亦無侵害系爭專利權之故意或過失」之理由進行抗辯。

（二）法院裁判
經法院依職權調查，於系爭工程的契約圖說所載之設計單位為訴外人名碁公司，並非被告友達公司或被告杰逸公司。再者，由於系爭工程僅對於被颱風侵襲損害之局部鋼棚屋頂作修復，依據臺東縣政府指示，為維持原有構造完整性及外觀一致性，訴外人名碁公司必須沿用訴外人OOO 建築師事務所之原始設計來辦理系爭工程之設計圖說。因此，系爭工程的設計與被告友達公司、杰逸公司無關。於是，法院認定被告友達公司係按名碁公司設計之系爭契約圖說進行施作，縱使施作之工作物侵害系爭專利權，亦難認其有侵害系爭專利權之故意或過失。另外，被告杰逸公司於工程中僅提供材料予被告友達公司，並未實際參與系爭工程之施作，故無侵害系爭專利權之行為。因此，本案原告敗訴，被告友達公司及杰逸公司均得以免除損害賠償責任。

（三）判例評析
1. 僅按圖施作不構成侵害專利權之故意或過失
如前所述，在承攬契約中的其中一種工作分配為，定作人在承攬契約中檢附詳細的物品或工程圖說，並給予相當的指示，而承攬人僅負責按圖施作。在系爭工程期間，承攬人友達公司對於系爭工程的施作並無主導權，僅能按照定作人臺東縣政府所提供之設計圖說及指示進行施作，否則將有可歸責之債務不履行事由。在此情況下，若被告友達公司仍須對設計內容進行專利檢索，確實太過嚴苛。因此，法院認定承攬人僅按圖施作不構成侵害專利權之故意或過失，有其道理。

2. 提供材料是否構成間接侵權行為
本案被告杰逸公司在系爭工程過程中僅轉售材料予被告友達公司，並未實際參與系爭工程之施作，無涉及專利法第58 條所規定的實施行為，因此被法院認定無侵害系爭專利權之行為。然而，如案例1 之第74 號判決中所論述，即使被控侵權人無涉及專利法第58 條所規定的實施行為，仍可能會構成客觀加害行為。因此，筆者認為僅以無涉及專利法第58 條所規定的實施行為即認定被告杰逸公司侵權不成立，似乎太過草率。相對地，筆者認為欲判斷被告杰逸公司侵權與否，必須考量以下兩個因素：首先，被告杰逸公司所提供的材料是否為製造侵權物品的重要材料；其次，被告杰逸公司在主觀上是否能意識到「提供材料」的行為可能侵害他人專利權。詳言之，若被告友達公司所需之材料為製造某一特定產品的重要材料，且身為材料供應商（雖原告主張被告杰逸公司為次承攬施作的廠商，但從法院調查結果來看，其性質應屬於材料供應商而非承攬商）的被告杰逸公司能知曉該產品受專利權保護，卻仍販售該材料予被告友達公司，則此時該販售材料的行為可能構成間接侵權行為。然而，從本案案情來看，被告杰逸公司販售予被告友達公司的材料非屬上述態樣，且被告杰逸公司在販售材料時也無法得知被告友達公司的施作行為是否會侵害他人專利權，此時若要求杰逸公司向友達公司探詢購買材料之目的，甚至是檢視友達公司所施作之工程項目是否會侵害他人專利權，並不合理。

總結上述，筆者認為「提供材料」雖無涉及專利法第58 條所規定的實施行為，但未必不會構成間接侵權行為，仍須考量上述因素再做出判斷較佳。另外，美國專利法第271 條第3 項中已明訂上述侵權態樣：「於美國境內為販賣之要約或販賣，或由外國輸入美國境內，屬已核准專利之機器、製品、組合物或化合物之重要成分，或實施已核准專利之方法所使用之材料或裝置，構成發明之重要部分，且明知該特別製造或特別使用係作為侵害該專利權，並非適用於實質上無侵害用途之主要物品（staplearticle）或商品者，應負輔助侵害人之責任」（輔助侵害）。因此，未來若欲就間接侵權之態樣對我國專利法進行修訂，或許能以美國專利法作為借鑑。

三、智慧財產法院110 年度民專訴字第41 號判決
（一）案情簡介
原告樂鑫開發工程有限公司為新型第M568885 號「水面灌漿平台吊掛裝置」專利（下稱系爭專利）之專利權人。被告宏華營造股份有限公司於108 年間承攬國防部之「左營港東5—東7 碼頭修建工程案」（下稱系爭修建工程）。

1. 原告主張
原告主張，被告原預計將系爭修建工程中的部分工程（下稱系爭碼頭工程）交由原告承攬，於是派員至原告處詢問系爭專利之細節。待原告提供系爭專利之細節資料後，被告隨即將系爭碼頭工程發包予訴外人杜貝特工程有限公司（下稱杜貝特公司）承攬施作，並指示杜貝特公司使用與系爭專利完全相同之施工方式進行施作。經鑑定後，原告認定系爭碼頭工程中所使用之吊掛組件落入系爭專利的權利範圍內，顯見被告有侵害系爭專利之行為及故意，應負損害賠償責任。
2. 被告抗辯
被告宏華公司略以「系爭修建工程雖由國防部發包予被告，然被告已將其中之系爭碼頭工程發包予杜貝特公司，故系爭碼頭工程之施工工法、使用材料，均由杜貝特公司提出並施作，被告對於系爭碼頭工程並無指示、干涉，自與被告無涉」之理由進行抗辯。

（二）法院裁判
經法院認定，依據原告所提出之LINE 對話截圖可證明原告於109 年間曾提供系爭專利之細節資料予被告宏華公司之負責人員，且證人杜貝特公司出庭時具結證稱在承攬系爭碼頭工程之前從未施作過碼頭工程，相關施工圖及設計圖皆為被告提供。據此，法院認定被告明知系爭專利為原告所有，卻未經其同意或授權即提供相關施工圖、設計圖予杜貝特公司，並指示杜貝特公司以與系爭專利相同方式施作系爭碼頭工程，從而有侵害系爭專利權之故意，應負損害賠償責任。

（三）判例評析
對於此判決，我們可再次看到法院並未就被告宏華公司是否涉及專利法第58 條所規定的「實施」行為去進行論述，而是就被告宏華公司對於侵權行為的發生是否具有主導權來認定侵權成立與否。被告宏華公司作為系爭碼頭工程的承攬人，對於系爭碼頭工程的設計細節具有主導權，卻以轉包工程做為誘因騙取原告之專利技術細節資料，並轉交該等資料予訴外人杜貝特公司進行施作。被告宏華公司在明知原告已取得專利權的情況下，不但沒有避免侵害原告之專利權，反而故意導致侵權行為的發生，而因此成立侵害系爭專利權之故意。

在智慧財產權意識逐漸高漲的時代，往往會與運行已久的制度產生摩擦、矛盾，其中承攬制度便是其中一種使專利侵權訴訟趨於複雜的例子。尤其，在我國設計專利之申請態樣放寬至建築工程領域的情況下，涉及承攬契約的專利侵權訴訟數量也可能隨之增加。因此，本文就三件涉及承攬契約的專利侵權訴訟判決加以分析，並且期望本文分析之內容能讓專利權人明白當專利侵權訴訟涉及承攬制度時，我國智財法院的立場為何，以及讓定作人及承攬廠商意識到其各自在承攬契約中分別具有何種程度的專利權注意義務。

根據本文所分析內容，當專利侵權行為涉及多人分工時，若定作人於定作或指示並無過失，或是承攬人僅是按照定作人所提供之設計圖施作時，法院認為該等情況不構成侵權之故意或過失；而在判斷被告是否構成侵權行為時，法院並不將侵權成立要件僅限於我國專利法第58 條所規定的「實施」行為，而是考量被控侵權人對於侵權行為的發生是否具有「主導權」。

另外，目前我國專利法僅明定直接侵權的態樣，當侵權行為涉及多人分工時，對於專利權人的法條適用並不直觀，舉證難度也隨之增加，而可能使專利權人的權益減損。因此，若未來專利法修訂能參照我國民法及他國專利法增訂直接侵權之外的侵權態樣，相信不僅能更加保障專利權人的權利，更能使專利侵權訴訟及法院裁判的體系更加健全。